Antibody-antigen modelling tutorial using a local version of HADDOCK3
This tutorial consists of the following sections:
- Introduction
- Setup/Requirements
- HADDOCK general concepts
- A brief introduction to HADDOCK3
- Software requirements
- Preparing PDB files for docking
- Defining restraints for docking
- Identifying the paratope of the antibody
- Antigen scenario 1: no information
- Antigen scenario 2: NMR-mapped epitope information
- Defining ambiguous restraints for scenario 1
- Defining ambiguous restraints for scenario 2a
- Defining ambiguous restraints for scenario 2b
- Additional restraints for multi-chain proteins
- Setting up the docking with HADDOCK3
- Analysis of docking results
- Visualization of the models
- Conclusions
- Congratulations! 🎉
- A look into the future Virtual Research Environment for HADDOCK3
Introduction
This tutorial demonstrates the use of the new modular HADDOCK3 version for predicting the structure of an antibody-antigen complex using knowledge of the hypervariable loops on the antibody and either the entire surface or an epitope identified from NMR chemical shift perturbation data for the antigen to guide the docking.
An antibody is a large protein that generally works by attaching itself to an antigen, which is a unique site of the pathogen. The binding harnesses the immune system to directly attack and destroy the pathogen. Antibodies can be highly specific while showing low immunogenicity, which is achieved by their unique structure. The fragment crystallizable region (Fc region) activates the immune response and is species-specific, i.e. the human Fc region should not induce an immune response in humans. The fragment antigen-binding region (Fab region) needs to be highly variable to be able to bind to antigens of various nature (high specificity). In this tutorial we will concentrate on the terminal variable domain (Fv) of the Fab region.
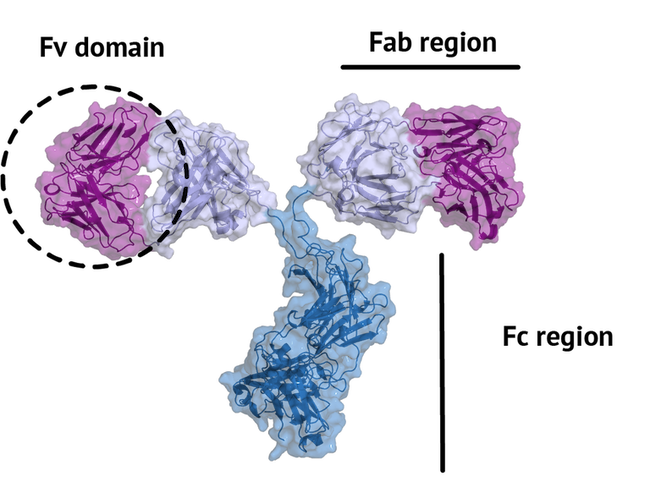
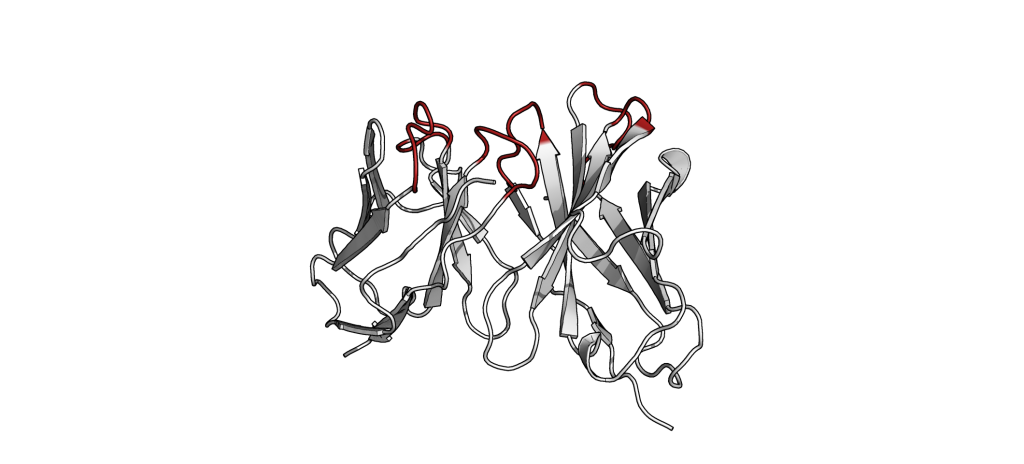
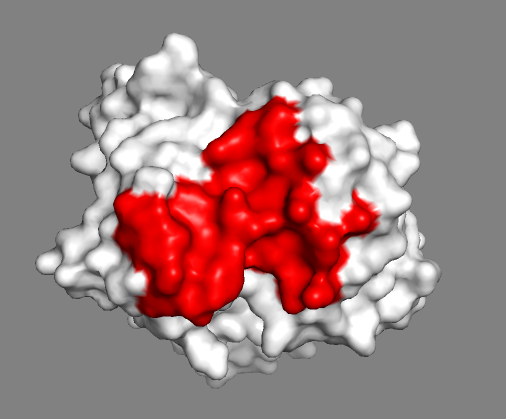
The small part of the Fab region that binds the antigen is called paratope. The part of the antigen that binds to an antibody is called epitope. The paratope consists of six highly flexible loops, known as complementarity-determining regions (CDRs) or hypervariable loops whose sequence and conformation are altered to bind to different antigens. CDRs are shown in red in the figure below:
In this tutorial we will be working with Interleukin-1β (IL-1β) (PDB code 4I1B) as an antigen and its highly specific monoclonal antibody gevokizumab (PDB code 4G6K) (PDB code of the complex 4G6M).
Throughout the tutorial, colored text will be used to refer to questions or instructions, and/or PyMOL commands.
This is a question prompt: try answering it! This an instruction prompt: follow it! This is a PyMOL prompt: write this in the PyMOL command line prompt! This is a Linux prompt: insert the commands in the terminal!
Setup/Requirements
In order to follow this tutorial you will need to work on a Linux or MacOSX system. We will also make use of PyMOL (freely available for most operating systems) in order to visualize the input and output data. We will provide you links to download the various required software and data.
Further we are providing pre-processed PDB files for docking and analysis (but the preprocessing of those files will also be explained in this tutorial). The files have been processed to facilitate their use in HADDOCK and for allowing comparison with the known reference structure of the complex. For this download and unzip the following zip archive and note the location of the extracted PDB files in your system. In it you should find the following directories:
haddock3: Contains HADDOCK3 configuration and job files for the various scenarios in this tutorialpdbs: Contains the pre-processed PDB filesplots: Contains pre-generated html plots for the various scenarios in this tutorialrestraints: Contains the interface information and the correspond restraint files for HADDOCKruns: Contains pre-calculated (partial) run results for the various scenarios in this tutorialscripts: Contains a variety of scripts used in this tutorial
Setup for the ISGC2023 HADDOCK workshop in Taipei
For this workshop we will be making use of the NMRBox resources. NMRbox offers cloud-based virtual machines for executing various biomolecular software that can complement NMR (Nuclear Magnetic Resonance). NMRbox users can choose from a large number of software packages that focus on research topics as metabolomics, molecular dynamics, structure, intrinsically disordered proteins or binding. One can search through all available packages on https://nmrbox.nmrhub.org/software.
Register on NMRBox
To use virtual machines through NMRbox, one needs to register, preferably with their institutional account here. Since the registration has to be manually validated and it can take up to two business days, we strongly encourage students to do so before the course starts. After a successful validation you will receive an e-mail with your NMRbox username and password that you will be using while accessing your virtual machine.
Accessing NMRbox
To run the virtual machine on a local computer, one needs to install VNCviewer. With the RealVNC client connects your computer to the NMRbox servers with a virtual desktop - graphical interface. More information about the VNC viewer is in the FAQ of NMRbox.
To choose a virtual machine, first log into the user dashboard https://nmrbox.nmrhub.org/user-dashboard. Download the zip file with bookmarks for the production NMRbox virtual machines. Click File -> Import connections and select the downloaded zip file. After importing, you will see the current release virtual machines. You can use any available virtual machine. The user-dashboard provides information on machine capabilities and recent compute load, thus it is clever to choose a less occupied one. Double click on one of the VMs. An “Authentication” panel appears. Enter your NMRbox username and password. Click on the “Remember password” box to have RealVNC save your information. By default, your desktop remains running when you disconnect from it. If you login to your VM repeatedly you will see a screen symbol next to the VM you connected to recently. For more details follow the quick start guide for using NMRbox with VNC viewer here.
If everything runs correctly you should have a window with your virtual desktop open. In the virtual desktop you have an access to the internet with Chromium as browser or use various programs, including Pymol. Thus, you could run all three stages of this course here or transfer data between your local machine and the virtual machine. File transfer to and from the VM is quite straightforward and it is described here: https://nmrbox.nmrhub.org/faqs/file-transfer.
In this workshop we will be working with the command line. For those of you who are not familiar with it, a lot of useful tutorials and documentation can be found here. To find the terminal, look for a black icon with a $_ symbol on it. Once you are familiar with the command line, you can start the tutorial.
Further NMRbox documentation can be found here.
Once you are done using your VM just log out of it using the top menu button as shown in this 9s video.
Important: In order to participate to the ISGC2023 HADDOCK workshop, once you have an account on NMRBox, make sure to register for the workshop on NMRBox. In that was all the data required for the workshop will be automatically copied to your home directory.
Tutorial setup on NMRbox
Connect to a NMRBox VM and open a terminal window
From the terminal setup the required environment (this activates haddock3) with:
source ~/EVENTS/2023-haddock-isgc-taipei/setup.sh
Then change directory to the workshop directory (the data have been copied automatically to your home dir if you registered for the event):
cd ~/EVENTS/2023-haddock-isgc-taipei/HADDOCK3-antibody-antigen
You will find in that directory all input and precalculatd data and scripts required to run this tutorial.
Setup for the 2022 EU-ASEAN HPC school on Fugaku
View details expand_more
The software and data required for this tutorial have been pre-installed on Fugaku. In order to run the tutorial, first copy the required data into your home directory on fugagku: tar xfz /vol0601/share/ra020021/LifeScience/20221208_Bonvin/HADDOCK3-antibody-antigen.tgz This will create the `HADDOCK3-antibody-antigen` directory with all necessary data and script and job examples ready for submission to the batch system. HADDOCK3 has been pre-installed, both on the login node and on the compute nodes. To active HADDOCK3 on the login node type: source /vol0601/share/ra020021/LifeScience/20221208_Bonvin/miniconda3/etc/profile.d/conda.shconda activate haddock3 You will now have all the require software in place to run the various steps of this tutorial. In case you would start an interactive session on a node, e.g. with the following command: pjsub \-\-interact \-\-sparam wait-time=60 \-L \"elapse=02:00:00\" \-x \"PJM_LLIO_GFSCACHE=/vol0003:/vol0006\" use then the following command to active the HADDOCK3 environment for the arm8 architecture of the compute nodes: source /vol0601/share/ra020021/LifeScience/20221208_Bonvin/miniconda3-arm8/etc/profile.d/conda.sh
conda activate haddock3 This is the command you will also find in the example job script for batch submission.
HADDOCK general concepts
HADDOCK (see https://www.bonvinlab.org/software/haddock2.4) is a collection of python scripts derived from ARIA (https://aria.pasteur.fr) that harness the power of CNS (Crystallography and NMR System – https://cns-online.org) for structure calculation of molecular complexes. What distinguishes HADDOCK from other docking software is its ability, inherited from CNS, to incorporate experimental data as restraints and use these to guide the docking process alongside traditional energetics and shape complementarity. Moreover, the intimate coupling with CNS endows HADDOCK with the ability to actually produce models of sufficient quality to be archived in the Protein Data Bank.
A central aspect to HADDOCK is the definition of Ambiguous Interaction Restraints or AIRs. These allow the translation of raw data such as NMR chemical shift perturbation or mutagenesis experiments into distance restraints that are incorporated in the energy function used in the calculations. AIRs are defined through a list of residues that fall under two categories: active and passive. Generally, active residues are those of central importance for the interaction, such as residues whose knockouts abolish the interaction or those where the chemical shift perturbation is higher. Throughout the simulation, these active residues are restrained to be part of the interface, if possible, otherwise incurring in a scoring penalty. Passive residues are those that contribute for the interaction, but are deemed of less importance. If such a residue does not belong in the interface there is no scoring penalty. Hence, a careful selection of which residues are active and which are passive is critical for the success of the docking.
A brief introduction to HADDOCK3
HADDOCK3 is the next generation integrative modelling software in the long-lasting HADDOCK project. It represents a complete rethinking and rewriting of the HADDOCK2.X series, implementing a new way to interact with HADDOCK and offering new features to users who can now define custom workflows.
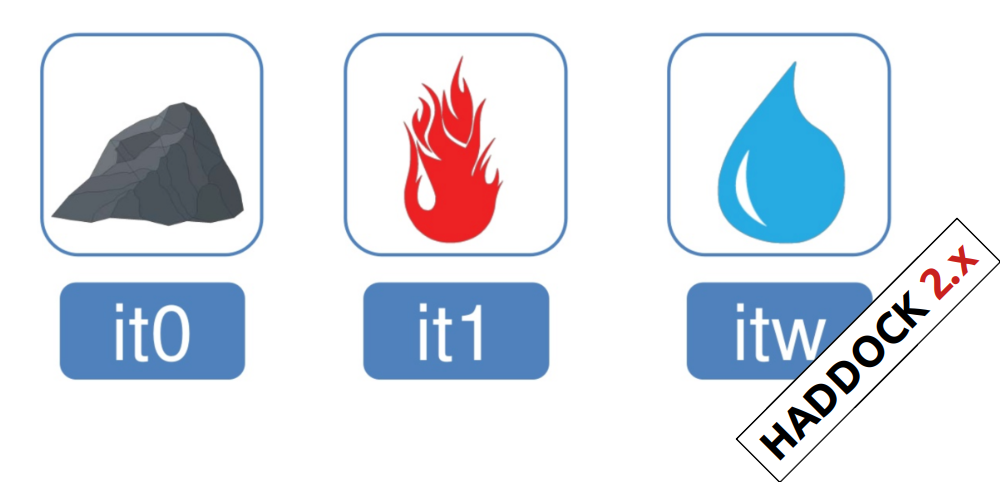
In the previous HADDOCK2.x versions, users had access to a highly
parameterisable yet rigid simulation pipeline composed of three steps:
rigid-body docking (it0), semi-flexible refinement (it1), and final refinement (itw).
In HADDOCK3, users have the freedom to configure docking workflows into
functional pipelines by combining the different HADDOCK3 modules, thus
adapting the workflows to their projects. HADDOCK3 has therefore developed to
truthfully work like a puzzle of many pieces (simulation modules) that users can
combine freely. To this end, the “old” HADDOCK machinery has been modularized,
and several new modules added, including third-party software additions. As a
result, the modularization achieved in HADDOCK3 allows users to duplicate steps
within one workflow (e.g., to repeat twice the it1 stage of the HADDOCK2.x
rigid workflow).
Note that, for simplification purposes, at this time, not all functionalities of HADDOCK2.x have been ported to HADDOCK3, which does not (yet) support NMR RDC, PCS and diffusion anisotropy restraints, cryo-EM restraints and coarse-graining. Any type of information that can be converted into ambiguous interaction restraints can, however, be used in HADDOCK3, which also supports the ab initio docking modes of HADDOCK.
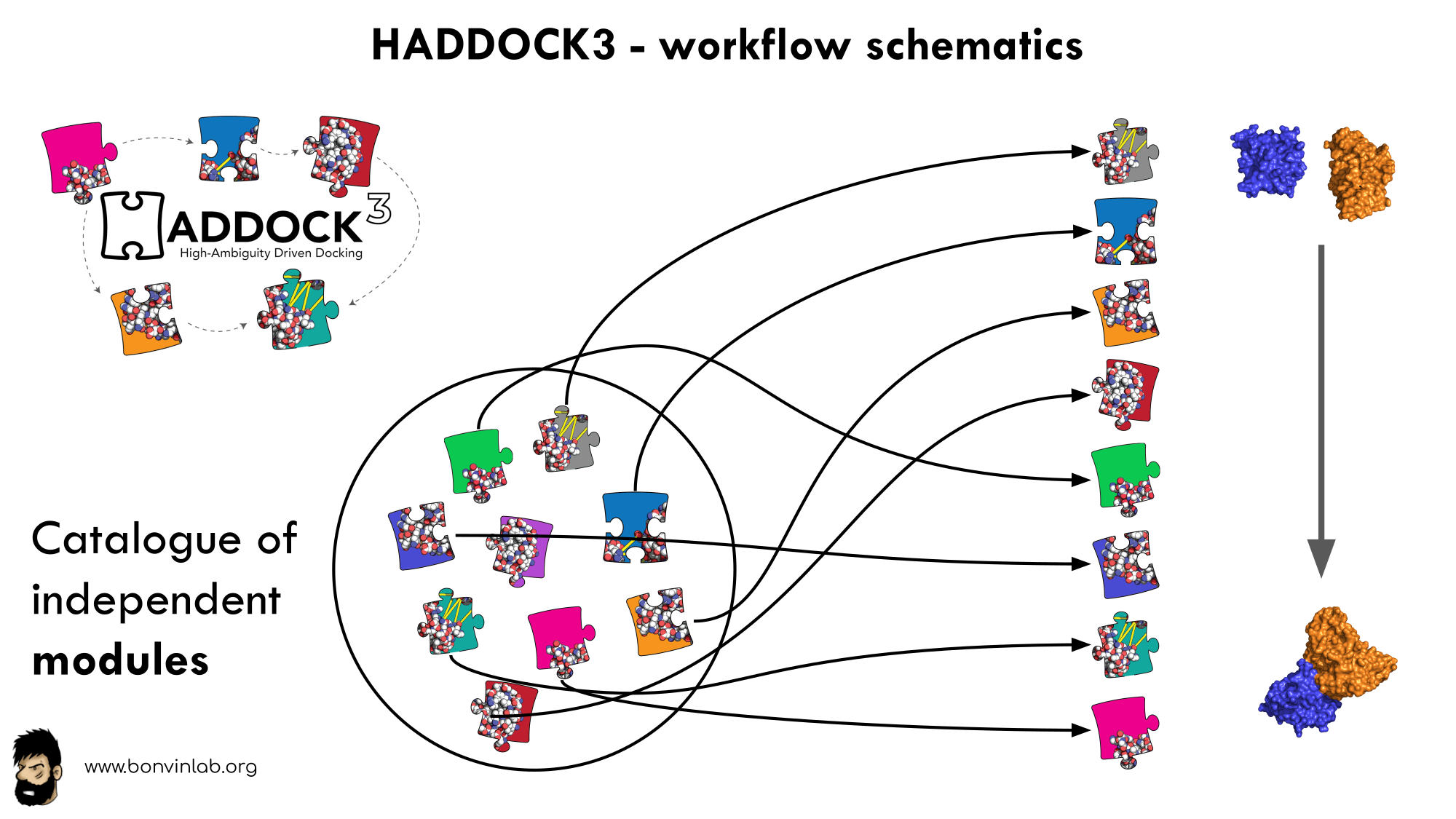
To keep HADDOCK3 modules organized, we catalogued them into several categories. But, there are no constraints on piping modules of different categories.
The main module categories are “topology”, “sampling”, “refinement”, “scoring”, and “analysis”. There is no limit to how many modules can belong to a category. Modules are added as developed, and new categories will be created if/when needed. You can access the HADDOCK3 documentation page for the list of all categories and modules. Below is a summary of the available modules:
- Topology modules
topoaa: generates the all-atom topologies for the CNS engine.
- Sampling modules
rigidbody: Rigid body energy minimization with CNS (it0in haddock2.x).lightdock: Third-party glow-worm swam optimization docking software.
- Model refinement modules
flexref: Semi-flexible refinement using a simulated annealing protocol through molecular dynamics simulations in torsion angle space (it1in haddock2.x).emref: Refinement by energy minimisation (itwEM only in haddock2.4).mdref: Refinement by a short molecular dynamics simulation in explicit solvent (itwin haddock2.X).
- Scoring modules
emscoring: scoring of a complex performing a short EM (builds the topology and all missing atoms).mdscoring: scoring of a complex performing a short MD in explicit solvent + EM (builds the topology and all missing atoms).
- Analysis modules
caprieval: Calculates CAPRI metrics (i-RMSD, l-RMSD, Fnat, DockQ) with respect to the top scoring model or reference structure if provided.clustfcc: Clusters models based on the fraction of common contacts (FCC)rmsdmatrix: Calculates the pairwise RMSD matrix between all the models generated in the previous step.ilrmsdmatrix: Calculates the pairwise interface-ligand RMSD matrix between all the models generated in the previous step.clustrmsd: Clusters models based on pairwise RMSD matrix calculated with thermsdmatrix/ilrmsdmatrixmodule.seletop: Selects the top N models from the previous step.seletopclusts: Selects top N clusters from the previous step.contactmap: Generates a contact map for the models generated in the previous step.alascan: Performs an alanine scanning on the models generated in the previous step.
The HADDOCK3 workflows are defined in simple configuration text files, similar to the TOML format but with extra features. Contrarily to HADDOCK2.X which follows a rigid (yet highly parameterisable) procedure, in HADDOCK3, you can create your own simulation workflows by combining a multitude of independent modules that perform specialized tasks.
Software requirements
Installing CNS
The other required piece of software to run HADDOCK is its computational engine,
CNS (Crystallography and NMR System –
https://cns-online.org). CNS is
freely available for non-profit organizations. In order to get access to all
features of HADDOCK you will need to compile CNS using the additional files
provided in the HADDOCK distribution in the varia/cns1.3 directory. Compilation of
CNS might be non-trivial. Some guidance on installing CNS is provided in the online
HADDOCK3 documentation page here.
Installing HADDOCK3
In this tutorial we will make use of the HADDOCK3 version. In case HADDOCK3 is not pre-installed in your system you will have to install it.
To obtain HADDOCK3 navigate to its repository, fill the registration form, and then follow the installation instructions.
Auxiliary software
FreeSASA: FreeSASA will be used to identify surface-accessible residues (pre-calculated data are provided).
PDB-tools: A useful collection of Python scripts for the
manipulation (renumbering, changing chain and segIDs…) of PDB files is freely
available from our GitHub repository. pdb-tools is automatically installed
with HADDOCK3. If you have activated the HADDOCK3 Python environment you have
access to the pdb-tools package.
PyMol: We will make use of PyMol for visualization. If not already installed on your system, download and install PyMol.
Preparing PDB files for docking
In this section we will prepare the PDB files of the antibody and antigen for docking.
Crystal structures of both the antibody and the antigen in their free forms are available from the
PDBe database. In the case of the antibody which consists
of two chains (L+H) we will have to prepare it for use in HADDOCK such as it can be treated as
a single chain with non-overlapping residue numbering. For this we will be making use of pdb-tools from the command line.
Note that pdb-tools is also available as a web service.
Note: Before starting to work on the tutorial, make sure to activate haddock3 (follow the workshop-specific instructions above), or, e.g. if installed using conda
Preparing the antibody structure
Using PDB-tools we will download the structure from the PDB database (the PDB ID is 4G6K) and then process it to have a unique chain ID (A) and non-overlapping residue numbering by shifting the residue numbering of the second chain.
This can be done from the command line with:
pdb_fetch 4G6K | pdb_tidy -strict | pdb_selchain -H | pdb_delhetatm | pdb_fixinsert | pdb_keepcoord | pdb_tidy -strict > 4G6K_H.pdb pdb_fetch 4G6K | pdb_tidy -strict | pdb_selchain -L | pdb_delhetatm | pdb_fixinsert | pdb_shiftres -1000 | pdb_keepcoord | pdb_tidy -strict > 4G6K_L.pdb pdb_merge 4G6K_H.pdb 4G6K_L.pdb |pdb_chain -A |pdb_chainxseg | pdb_tidy -strict > 4G6K_clean.pdb
The first command fetches the PDB ID, select the heavy chain (H) and removes water and heteroatoms (in this case no co-factor is present that should be kept).
An important part for antibodies is the pdb_fixinsert command that fixes the residue numbering of the HV loops: Antibodies often follow the Chothia numbering scheme and insertions created by this numbering scheme (e.g. 82A,82B,82C) cannot be processed by HADDOCK directly. As such renumbering is necessary before starting the docking.
The second command does the same for the light chain (L) with an additional step of shifting the residue numbering by 1000 (using pdb_shiftres) to avoid overlap in the numbering of the two chains.
The third and last command merges the two processed chains and assign them unique chain- and segIDs, resulting in the HADDOCK-ready 4G6K_clean.pdb file.
Note that the corresponding files can be found in the pdbs directory of the archive you downloaded.
Preparing the antigen structure
Using PDB-tools we will download the structure from the PDB database (the PDB ID is 4I1B), remove the hetero atoms and then process it to assign it chainID B.
Defining restraints for docking
Before setting up the docking we need first to generate distance restraint files in a format suitable for HADDOCK. HADDOCK uses CNS as computational engine. A description of the format for the various restraint types supported by HADDOCK can be found in our Nature Protocol paper, Box 4.
Distance restraints are defined as:
assign (selection1) (selection2) distance, lower-bound correction, upper-bound correction
The lower limit for the distance is calculated as: distance minus lower-bound
correction and the upper limit as: distance plus upper-bound correction. The
syntax for the selections can combine information about chainID - segid
keyword -, residue number - resid keyword -, atom name - name keyword.
Other keywords can be used in various combinations of OR and AND statements.
Please refer for that to the online CNS manual.
We will shortly explain in this section how to generate both ambiguous interaction restraints (AIRs) and specific distance restraints for use in HADDOCK illustrating two scenarios:
- HV loops on the antibody, full surface on the antigen
- HV loops on the antibody, NMR interface mapping on the antigen
Information about various types of distance restraints in HADDOCK can also be found in our online manual pages.
Identifying the paratope of the antibody
Nowadays there are several computational tools that can identify the paratope (the residues of the hypervariable loops involved in binding) from the provided antibody sequence. In this tutorial we are providing you the corresponding list of residue obtained using ProABC-2. ProABC-2 uses a convolutional neural network to identify not only residues which are located in the paratope region but also the nature of interactions they are most likely involved in (hydrophobic or hydrophilic). The work is described in Ambrosetti, et al Bioinformatics, 2020.
The corresponding paratope residues (those with either an overall probability >= 0.4 or a probability for hydrophobic or hydrophilic > 0.3) are:
31,32,33,34,35,52,54,55,56,100,101,102,103,104,105,106,1031,1032,1049,1050,1053,1091,1092,1093,1094,1096
The numbering corresponds to the numbering of the 4G6K_clean.pdb PDB file.
Let us visualize those onto the 3D structure.
For this start PyMOL and load 4G6K_clean.pdb
File menu -> Open -> select 4G6K_clean.pdb
or from the command line:
We will now highlight the predicted paratope. In PyMOL type the following commands:
color white, all
select paratope, (resi 31+32+33+34+35+52+54+55+56+100+101+102+103+104+105+106+1031+1032+1049+1050+1053+1091+1092+1093+1094+1096)
color red, paratope
Let us now switch to a surface representation to inspect the predicted binding site.
Inspect the surface.
Do the identified residues form a well defined patch on the surface?
See surface view of the paratope expand_more
Antigen scenario 1: no information
In this scenario, we will target the entire surface of the antigen by selecting the solvent accessible residues.
For this can use freesasa to calculate the solvent accessible surface area (SASA) for the different
residues. If freesasa is available from the command line you can run it to generate the solvent accessibility data with:
freesasa 4I1B_clean.pdb --format=rsa >4I1B_clean.rsa
REM FreeSASA 2.0.3 REM Absolute and relative SASAs for 4I1B_clean.pdb REM Atomic radii and reference values for relative SASA: ProtOr REM Chains: A REM Algorithm: Lee & Richards REM Probe-radius: 1.40 REM Slices: 20 REM RES _ NUM All-atoms Total-Side Main-Chain Non-polar All polar REM ABS REL ABS REL ABS REL ABS REL ABS REL RES VAL A 3 84.83 55.8 13.08 11.8 71.76 172.9 30.45 26.5 54.38 147.5 RES ARG A 4 200.36 84.1 192.85 98.3 7.51 17.9 71.92 98.3 128.44 77.8 RES SER A 5 48.69 41.1 25.55 34.1 23.14 53.3 22.44 47.8 26.25 36.8 RES LEU A 6 71.91 40.0 70.87 50.7 1.04 2.6 71.91 50.5 0.00 0.0 RES ASN A 7 31.01 21.4 25.87 25.0 5.14 12.4 0.00 0.0 31.01 30.0 ...
The following command will return all residues with a relative SASA for either the backbone or the side-chain > 15% (we use 15% to limit the number of surface residues selected as their number does increase the computational requirements)
The resulting list of residues can be found in the restraints/antigen-surface.act-pass file. Note in this file the empty first line. The file consists
of two lines, with the first one defining the active residues and the second line the passive ones, in this case the solvent accessible residues.
We will use later this file to generate the ambiguous distance restraints for HADDOCK.
If you want to generate the same file, first create an empty line and then use the awk command, piping the results to an output file, e.g.:
The same can be achieved using the haddock3-restraints command line tool:
haddock3-restraints calc_accessibility –cutoff 0.15 pdbs/4I1B_clean.pdb
The simple output directly reports the list of residues:
14/03/2023 13:15:20 L157 INFO - Calculate accessibility... 14/03/2023 13:15:20 L228 INFO - Chain: B - 151 residues 14/03/2023 13:15:20 L234 INFO - Applying cutoff to side_chain_rel - 0.15 14/03/2023 13:15:20 L244 INFO - Chain B - 3,4,5,6,7,11,13,14,15,20,21,22,23,24,25,27,29,30,32,33,34,35,36,37,38,41,43,46,48,49,50,51,52,53,54,55,56,63,64,65,66,72,73,74,75,76,77,79,81,83,84,86,87,88,89,91,92,93,94,96,97,98,105,106,107,108,109,115,116,117,118,119,120,125,126,127,128,129,130,131,133,135,137,138,139,140,141,142,145,147,149,150,151,152,153
We can visualize the selected surface residues of Interleukin-1β.
For this start PyMOL and from the PyMOL File menu open the PDB file of the antigen.
color white, all show surface select surface15, (resi 3+4+5+6+13+14+15+20+21+22+23+24+25+30+32+33+34+35+37+38+48+49+50+51+52+53+54+55+61+63+64+65+66+73+74+75+76+77+80+84+86+87+88+89+90+91+93+94+96+97+105+106+107+108+109+118+119+126+127+128+129+130+135+136+137+138+139+140+141+142+147+148+150+151+152+153) color green, surface40
color white, all show surface select surface40, (resi 3+4+5+6+13+14+15+20+21+22+23+24+25+30+32+33+34+35+37+38+48+49+50+51+52+53+54+55+61+63+64+65+66+73+74+75+76+77+80+84+86+87+88+89+90+91+93+94+96+97+105+106+107+108+109+118+119+126+127+128+129+130+135+136+137+138+139+140+141+142+147+148+150+151+152+153) color green, surface40
Antigen scenario 2: NMR-mapped epitope information
The article describing the crystal structure of the antibody-antigen complex we are modelling also reports on experimental NMR chemical shift titration experiments to map the binding site of the antibody (gevokizumab) on Interleukin-1β. The residues affected by binding are listed in Table 5 of Blech et al. JMB 2013:
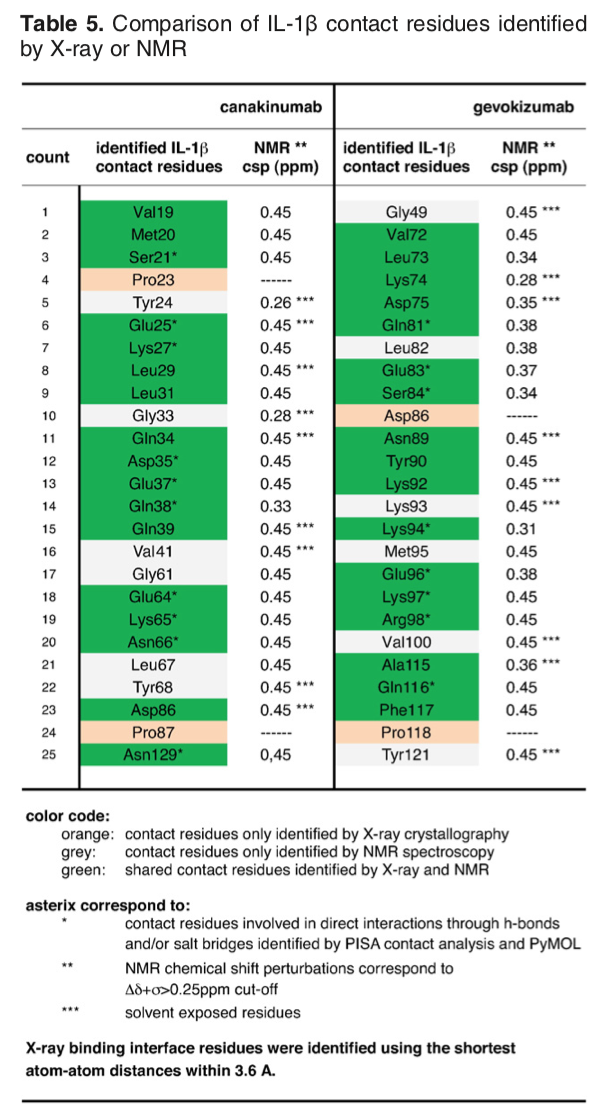
The list of binding site (epitope) residues identified by NMR is:
72,73,74,75,81,83,84,89,90,92,94,96,97,98,115,116,117
We will now visualize the epitope on Interleukin-1β. For this start PyMOL and from the PyMOL File menu open the provided PDB file of the antigen.
File menu -> Open -> select 4I1B_clean.pdb
color white, all show surface select epitope, (resi 72+73+74+75+81+83+84+89+90+92+94+96+97+98+115+116+117) color red, epitope
Inspect the surface.
Do the identified residues form a well defined patch on the surface?
The answer to that question should be yes, but we can see some residues not colored that might also be involved in the binding - there are some white spots around/in the red surface.
See surface view of the epitope identified by NMR expand_more

In HADDOCK we are dealing with potentially incomplete binding sites by defining surface neighbors as passive residues.
These are added to the definition of the interface but will not lead to any energetic penalty if they are not part of the
binding site in the final models, while the residues defined as active (typically the identified or predicted binding
site residues) will. When using the HADDOCK server, passive residues will be automatically defined. Here since we are
using a local version, we need to define those manually.
This can easily be done using the following HADDOCK3 command line interface:
The NMR-identified residues and their surface neighbors generated with the above command can be used to define ambiguous interactions restraints, either using the NMR identified residues as active in HADDOCK, or combining those with the surface neighbors and use this combination as passive only.
The corresponding files can be found in the restraints/antigen-NMR-epitope.act-pass and restraints/antigen-NMR-epitope.passfiles.
Note in the second file the empty first line. The file consists of two lines, with the first one defining the active residues and
the second line the passive ones. We will use later these files to generate the ambiguous distance restraints for HADDOCK.
In general it is better to be too generous rather than too strict in the definition of passive residues.
An important aspect is to filter both the active (the residues identified from your mapping experiment) and passive residues by their solvent accessibility. Our web service uses a default relative accessibility of 15% as cutoff. This is not a hard limit. You might consider including even more buried residues if some important chemical group seems solvent accessible from a visual inspection.
Defining ambiguous restraints for scenario 1
Once you have defined your active and passive residues for both molecules, you
can proceed with the generation of the ambiguous interaction restraints (AIR) file for HADDOCK.
For this you can either make use of our online GenTBL web service, entering the
list of active and passive residues for each molecule, and saving the resulting
restraint list to a text file, or use the relevant haddock-tools script.
To use our haddock3-restraints active_passive_to_ambig script you need to
create for each molecule a file containing two lines:
- The first line corresponds to the list of active residues (numbers separated by spaces)
- The second line corresponds to the list of passive residues.
For scenario 1 this would be:
- For the antibody (the file called
antibody-paratope.act-passfrom therestraintsdirectory):
31 32 33 34 35 52 54 55 56 100 101 102 103 104 105 106 1031 1032 1049 1050 1053 1091 1092 1093 1094 1096
- and for the antigen (the file called
antigen-surface.passfrom therestraintsdirectory):
3 4 5 6 13 14 15 20 21 22 23 24 25 30 32 33 34 35 37 38 48 49 50 51 52 53 54 55 61 63 64 65 66 73 74 75 76 77 80 84 86 87 88 89 90 91 93 94 96 97 105 106 107 108 109 118 119 126 127 128 129 130 135 136 137 138 139 140 141 142 147 148 150 151 152 153
Using those two files, we can generate the CNS-formatted AIR restraint files with the following command:
This generates a file called ambig-paratope-surface.tbl that contains the AIR
restraints. The default distance range for those is between 0 and 2Å, which
might seem short but makes senses because of the 1/r^6 summation in the AIR
energy function that makes the effective distance be significantly shorter than
the shortest distance entering the sum.
The effective distance is calculated as the SUM over all pairwise atom-atom distance combinations between an active residue and all the active+passive on the other molecule: SUM[1/r^6]^(-1/6).
If you modify manually this file, it is possible to quickly check if the format is valid.
To do so, you can use the haddock3-restraints validate_tbl utility.
To use it, type:
haddock3-restraints validate_tbl --silent ambig-paratope-surface.tbl
No output means that your TBL file is valid.
Defining ambiguous restraints for scenario 2a
In this scenario the NMR epitope combined with the surface neighbors are used as passive residues in HADDOCK.
The creation of the AIR tbl file for scenario 2a is similar to scenario 1, but instead using the antigen-NMR-epitope.pass file for the antigen:
Defining ambiguous restraints for scenario 2b
In this scenario the NMR epitope is defined as active (meaning ambiguous distance restraints will be defined from the NMR epitope residues) and the surface neighbors are used as passive residues in HADDOCK.
The creation of the AIR tbl file for scenario 2b is similar to scenario 1, but instead using the antigen-NMR-epitope.act-pass file for the antigen:
Additional restraints for multi-chain proteins
As an antibody consists of two separate chains, it is important to define a few distance restraints
to keep them together during the high temperature flexible refinement stage of HADDOCK. This can easily be
done using another haddock3-restraints subcommand.
haddock3-restraints restrain_bodies 4G6K_clean.pdb > antibody-unambig.tbl
The result file contains two CA-CA distance restraints with the exact distance measured between the picked CA atoms:
assign (segid A and resi 220 and name CA) (segid A and resi 1018 and name CA) 47.578 0.0 0.0 assign (segid A and resi 193 and name CA) (segid A and resi 1014 and name CA) 33.405 0.0 0.0
This file is also provided in the restraints directory of the archive you downloaded.
Setting up the docking with HADDOCK3
Now that we have all required files at hand (PBD and restraints files) it is time to setup our docking protocol. For this we need to create a HADDOCK3 configuration file that will define the docking workflow. In contrast to HADDOCK2.X, we have much more flexibility in doing this. We will illustrate this flexibility by introducing a clustering step after the initial rigid-body docking stage, select up to 10 models per cluster and refine all of those.
HADDOCK3 also provides an analysis module (caprieval) that allows
to compare models to either the best scoring model (if no reference is given) or a reference structure, which in our case
we have at hand. This will directly allow us to assess the performance of the protocol for the following three scenarios:
- Scenario 1: Docking using the paratope information only and the surface of the antigen
- Scenario 2a: Docking using the paratope and the NMR-identified epitope as passive
- Scenario 2b: Docking using the paratope and the NMR-identified epitope as active
The basic workflow for all three scenarios will consists of the following modules, with some differences in the restraints used and some parameter settings (see below):
topoaa: Generates the topologies for the CNS engine and build missing atomsrigidbody: Rigid body energy minimisation (it0in haddock2.x)clustfcc: Clustering of models based on the fraction of common contacts (FCC)seletopclusts: Selection of the top10 models of all clustersflexref: Semi-flexible refinement of the interface (it1in haddock2.4)emref: Final refinement by energy minimisation (itwEM only in haddock2.4)clustfcc: Clustering of models based on the fraction of common contacts (FCC)caprieval: Calculates CAPRI metrics (i-RMSD, l-RMSD, Fnat, DockQ) with respect to the top scoring model or reference structure if provided
The input PDB files are the same for all three scenarios. The differences are in the ambiguous interaction restraint files used and the sampling at the rigid body stage in the case of scenario1.
Note that for the** ISGC2023 HADDOCK workshop **, we will only run scenario2a with a reduced sampling for the rigid body module of 200 models to limit to the computing time and get results within a reasonable time using only 10 processors. The corresponding haddock3 scripts for this is provided as scenario2a-NMR-epitope-pass-short.cfg.
Other example scripts can be found in the haddock3 directory.
HADDOCK3 execution modes
HADDOCK3 currently supports three difference execution modes that are defined in the first section of the configuration file of a run.
1. local mode
In this mode HADDOCK3 will run on the current system, using the defined number of cores (ncores) in the config file
to a maximum of the total number of available cores on the system minus one. An example of the relevant parameters to be defined in the first section of the config file is:
# compute mode
mode = "local"
# 1 nodes x 96 ncores
ncores = 96In this mode HADDOCK3 can be started from the command line with as argument the configuration file of the defined workflow.
haddock3 <my-workflow-configuration-file>
Alternatively redirect the output to a log file and send haddock3 to the background.
Note: This is the execution mode you should use on the NMRBox resources. For the tutorial we limit the number of cores to 10.
haddock3 <my-workflow-configuration-file> > haddock3.log &
Note: This is also the execution mode that should be used for example when submitting the HADDOCK3 job to a node of a cluster, requesting X number of cores.
View an example script for submitting via the slurm batch system expand_more
#!/bin/bash
#SBATCH --nodes=1
#SBATCH --tasks-per-node=96
#SBATCH -J haddock3
#SBATCH --partition=medium
# load haddock3 module
module load haddock3
# or activate the haddock3 conda environment
##source $HOME/miniconda3/etc/profile.d/conda.sh
##conda activate haddock3
# go to the run directory
cd $HOME/HADDOCK3-antibody-antigen
# execute
haddock3 scenario1-surface-node.cfg
View an EU-ASEAN HPC school example script for submitting to the Fugaku batch system expand_more
#!/bin/bash
#PJM -L "node=1" # Assign 1 node
#PJM -L "elapse=02:00:00" # Elapsed time limit 2 hour
#PJM -x PJM_LLIO_GFSCACHE=/vol0003:/vol0006 # volume names that job uses
#PJM -s # Statistical information output
# active the haddock3 conda environment
source /vol0601/share/ra020021/LifeScience/20221208_Bonvin/miniconda3-arm8/etc/profile.d/conda.sh
conda activate haddock3
# go to the tutorial directory in your home directory
# edit if needed to specify the correct location
cd $HOME/HADDOCK3-antibody-antigen
# execute haddock3
haddock3 scenario2a-NMR-epitope-pass-node.cfg2. batch mode
In this mode HADDOCK3 will typically be started on your local server (e.g. the login node) and will dispatch jobs to the batch system of your cluster.
Two batch systems are currently supported: slurm and torque (defined by the batch_type parameter). In the configuration file you will
have to define the queue name and the maximum number of concurrent jobs sent to the queue (queue_limit). Since HADDOCK3 single model
calculations are quite fast, it is recommended to calculate multiple models within one job submitted to the batch system.
The number of model per job is defined by the concat parameter in the configuration file.
You want to avoid sending thousands of very short jobs to the batch system if you want to remain friend with your system administrators…
An example of the relevant parameters to be defined in the first section of the config file is:
# compute mode
mode = "batch"
# batch system
batch_type = "slurm"
# queue name
queue = "short"
# number of concurrent jobs to submit to the batch system
queue_limit = 100
# number of models to produce per submitted job
concat = 10In this mode HADDOCK3 can be started from the command line as for the local mode.
3. MPI mode
HADDOCK3 supports a parallel MPI implementation (functional but still very experimental at this stage). For this to work, the mpi4py library
must have been installed at installation time. Refer to the MPI-related instructions.
The execution mode should be set to mpi and the total number of cores should match the requested resources when submitting to the batch system.
An example of the relevant parameters to be defined in the first section of the config file is:
# compute mode
mode = "mpi"
# 5 nodes x 50 tasks = ncores = 250
ncores = 250In this execution mode the HADDOCK3 job should be submitted to the batch system requesting the corresponding number of nodes and cores per node.
View an example script for submitting an MPI HADDOCK3 job the slurm batch system expand_more
#!/bin/bash
#SBATCH --nodes=5
#SBATCH --tasks-per-node=50
#SBATCH -J haddock3mpi
# load haddock3 module
module load haddock3
# or make sure haddock3 is activated
##source $HOME/miniconda3/etc/profile.d/conda.sh
##conda activate haddock3
# go to the run directory
# edit if needed to specify the correct location
cd $HOME/HADDOCK3-antibody-antigen
# execute
haddock3 scenario2a-NMR-epitope-pass-mpi.cfg
Scenario 1: Paratope - antigen surface
Now that we have all data ready, and know about execution modes of HADDOCK3 it is time to setup the docking for the first scenario in which we will use the paratope on the antibody to guide the docking, targeting the entire surface of the antibody. The restraint file to use for this is ambig-paratope-surface.tbl. We will also define the restraints to keep the two antibody chains together using for this the antibody-unambig.tbl restraint file. Further, as we have no information on the antigen side, it is important to increase the sampling in the rigid body sampling stage to 10000. And we will also turn off the default random removal of restraints to keep all the information on the paratope (randremoval = false). The configuration file for this scenario (assuming a local running mode, eventually submitted to the batch system requesting a full node) is:
# ====================================================================
# Antibody-antigen docking example with restraints from the antibody
# paratope to the entire surface of the antigen
# ====================================================================
# directory name of the run
run_dir = "scenario1-surface"
# compute mode
mode = "local"
# 1 nodes x 96 threads
ncores = 96
# Self contained rundir (to avoid problems with long filename paths)
self_contained = true
# molecules to be docked
molecules = [
"pdbs/4G6K_clean.pdb",
"pdbs/4I1B_clean.pdb"
]
# ====================================================================
# Parameters for the various stages
# ====================================================================
[topoaa]
[rigidbody]
# CDR to surface ambig restraints
ambig_fname = "restraints/ambig-paratope-surface.tbl"
# Restraints to keep the antibody chains together
unambig_fname = "restraints/antibody-unambig.tbl"
# Turn off random removal of restraints
randremoval = false
# Number of models to generate
sampling = 10000
[clustfcc]
min_population = 4
top_models = 10
[seletopclusts]
## select all the clusters
top_cluster = 500
## select the best 10 models of each cluster
top_models = 10
[caprieval]
# this is only for this tutorial to check the performance at the rigidbody stage
reference_fname = "pdbs/4G6M_matched.pdb"
[flexref]
# Acceptable percentage of model failures
tolerance = 5
# CDR to surface ambig restraints
ambig_fname = "restraints/ambig-paratope-surface.tbl"
# Restraints to keep the antibody chains together
unambig_fname = "restraints/antibody-unambig.tbl"
# Turn off random removal of restraints
randremoval = false
[emref]
# CDR to surface ambig restraints
ambig_fname = "restraints/ambig-paratope-surface.tbl"
# Restraints to keep the antibody chains together
unambig_fname = "restraints/antibody-unambig.tbl"
# Turn off random removal of restraints
randremoval = false
[clustfcc]
[seletopclusts]
top_cluster = 500
[caprieval]
reference_fname = "pdbs/4G6M_matched.pdb"
# ====================================================================This configuration file is provided in the haddock3 directory of the downloaded data set for this tutorial as scenario1-surface-node.cfg.
An MPI version (this is still very much experimental and might not work on all systems) is also available as scenario1-surface-mpi.cfg.
If you have everything ready, you can launch haddock3 either from the command line, or, better, submitting it to the batch system requesting in this local run mode a full node (see local execution mode above).
Note that this scenario is computationally more expensive because of the increased sampling. On our own cluster, running in MPI mode with 250 cores on AMD EPYC 7451 processors the run completed in 1h23min. The same run on a single node using all 96 threads took on the same architecture 4 hours and 8 minutes.
On the Fugaku supercomputer used for the EU ASEAN HPC school, running on a single node 48 armv8 A64FX, this run completed in about 23 hours.
Scenario 2a: Paratope - NMR-epitope as passive
In scenario 2a we are setting up the docking in which the paratope on the antibody is used to guide the docking, targeting the NMR-identified epitope (+surface neighbors) defined as passive residues. The restraint file to use for this is ambig-paratope-NMR-epitope-pass.tbl. As for scenario1, we will also define the restraints to keep the two antibody chains together using for this the antibody-unambig.tbl restraint file. In this case since we have information for both interfaces default sampling parameters are sufficient. And we will also turn off the default random removal of restraints to keep all the information on the paratope (randremoval = false). The configuration file for this scenario (assuming a local running mode, eventually submitted to the batch system requesting a full node) is:
# ====================================================================
# Antibody-antigen docking example with restraints from the antibody
# paratope to the NMR-identified epitope on the antigen (as passive)
# ====================================================================
# directory name of the run
run_dir = "scenario2a-NMR-epitope-pass"
# MPI compute mode
mode = "local"
# 1 nodes x 96 threads
ncores = 96
# Self contained rundir (to avoid problems with long filename paths)
self_contained = true
# molecules to be docked
molecules = [
"pdbs/4G6K_clean.pdb",
"pdbs/4I1B_clean.pdb"
]
# ====================================================================
# Parameters for each stage are defined below, prefer full paths
# ====================================================================
[topoaa]
[rigidbody]
# CDR to surface ambig restraints
ambig_fname = "restraints/ambig-paratope-NMR-epitope-pass.tbl"
# Restraints to keep the antibody chains together
unambig_fname = "restraints/antibody-unambig.tbl"
# Turn off random removal of restraints
randremoval = false
[clustfcc]
min_population = 4
top_models = 10
[seletopclusts]
## select all the clusters
top_cluster = 500
## select the best 10 models of each cluster
top_models = 10
[caprieval]
# this is only for this tutorial to check the performance at the rigidbody stage
reference_fname = "pdbs/4G6M_matched.pdb"
[flexref]
# Acceptable percentage of model failures
tolerance = 5
# CDR to surface ambig restraints
ambig_fname = "restraints/ambig-paratope-NMR-epitope-pass.tbl"
# Restraints to keep the antibody chains together
unambig_fname = "restraints/antibody-unambig.tbl"
# Turn off random removal of restraints
randremoval = false
[emref]
# CDR to surface ambig restraints
ambig_fname = "restraints/ambig-paratope-NMR-epitope-pass.tbl"
# Restraints to keep the antibody chains together
unambig_fname = "restraints/antibody-unambig.tbl"
# Turn off random removal of restraints
randremoval = false
[clustfcc]
[seletopclusts]
top_cluster = 500
[caprieval]
reference_fname = "pdbs/4G6M_matched.pdb"
# ====================================================================This configuration is provided in the haddock3 directory of the downloaded data set for this tutorial as scenario2a-NMR-epitope-pass-node.cfg. An MPI version (this is still very much experimental and might not work on all systems) is also available as scenario2a-NMR-epitope-pass-mpi.cfg.
If you have everything ready, you can launch haddock3 either from the command line, or, better, submitting it to the batch system requesting in this local run mode a full node (see local execution mode above).
Note that this scenario is less expensive since we keep the default sampling parameters. On our own cluster, running in MPI mode with 250 cores on AMD EPYC 7451 processors the run completed in about 7 minutes. The same run on a single node using all 96 threads took on the same architecture about 21 minutes. In batch mode, using 100 queue slots and 10 models per job, the same run completed in about 45 minutes.
On the Fugaku supercomputer used for the EU ASEAN HPC school, running on a single node (48 armv8 A64FX processors), this run completed in about 1 hour and 15 minutes. Limiting the sampling to 240 rigid body models (recommended for the EU ASEAN HPC school) shorten the execution time to 37 minutes.
Scenario 2b: Paratope - NMR-epitope as active
Scenario 2b is rather similar to scenario 2a with the difference that the NMR-identified epitope is treated as active, meaning restraints will be defined from it to “force” it to be at the interface.
And since there might be more false positive data in the identified interfaces, we will leave the random removal of restraints on. The restraint file to use for this is ambig-paratope-NMR-epitope-act.tbl. As for scenario1, we will also define the restraints to keep the two antibody chains together using for this the antibody-unambig.tbl restraint file. In this case since we have information for both interfaces default sampling parameters are sufficient. The configuration file for this scenario (assuming a local running mode, eventually submitted to the batch system requesting a full node) is:
# ====================================================================
# Antibody-antigen docking example with restraints from the antibody
# paratope to the NMR-identified epitope on the antigen (as active)
# and keeping the random removal of restraints
# ====================================================================
# directory name of the run
run_dir = "scenario2b-NMR-epitope-act"
# compute mode
mode = "local"
# 1 nodes x 96 cores
ncores = 96
# Self contained rundir (to avoid problems with long filename paths)
self_contained = true
# molecules to be docked
molecules = [
"pdbs/4G6K_clean.pdb",
"pdbs/4I1B_clean.pdb"
]
# ====================================================================
# Parameters for each stage are defined below, prefer full paths
# ====================================================================
[topoaa]
[rigidbody]
# CDR to surface ambig restraints
ambig_fname = "restraints/ambig-paratope-NMR-epitope-act.tbl"
# Restraints to keep the antibody chains together
unambig_fname = "restraints/antibody-unambig.tbl"
[clustfcc]
min_population = 4
top_models = 10
[seletopclusts]
## select all the clusters
top_cluster = 500
## select the best 10 models of each cluster
top_models = 10
[caprieval]
# this is only for this tutorial to check the performance at the rigidbody stage
reference_fname = "pdbs/4G6M_matched.pdb"
[flexref]
# Acceptable percentage of model failures
tolerance = 5
# CDR to surface ambig restraints
ambig_fname = "restraints/ambig-paratope-NMR-epitope-act.tbl"
# Restraints to keep the antibody chains together
unambig_fname = "restraints/antibody-unambig.tbl"
[emref]
# CDR to surface ambig restraints
ambig_fname = "restraints/ambig-paratope-NMR-epitope-act.tbl"
# Restraints to keep the antibody chains together
unambig_fname = "restraints/antibody-unambig.tbl"
[clustfcc]
[seletopclusts]
top_cluster = 500
[caprieval]
reference_fname = "pdbs/4G6M_matched.pdb"
# ====================================================================This configuration file is provided in the haddock3 directory of the downloaded data set for this tutorial as scenario2b-NMR-epitope-act-node.cfg. An MPI version is also available as scenario2b-NMR-epitope-act-mpi.cfg.
If you have everything ready, you can launch haddock3 either from the command line, or, better, submitting it to the batch system requesting in this local run mode a full node (see local execution mode above).
Note The running time for this scenario is similar to that of scenario 2a (see above).
Analysis of docking results
Structure of the run directory
Once your run has completed inspect the content of the resulting directory. You will find the various steps (modules) of the defined workflow numbered sequentially, e.g.:
> ls scenario2a-NMR-epitope-pass/
0_topoaa/
1_rigidbody/
2_clustfcc/
3_seletopclusts/
4_caprieval/
5_flexref/
6_emref/
7_clustfcc/
8_seletopclusts/
9_caprieval/
analysis/
data/
logThere is in addition the log file (text file) and two additional directories:
- the
datadirectory containing the input data (PDB and restraint files) for the various modules - the
analysisdirectory containing various plots to visualise the results for eachcaprievalstep
You can find information about the duration of the run at the bottom of the log file. Each sampling/refinement/selection module will contain PBD files.
For example, the X_seletopclusts directory contains the selected models from each cluster. The clusters in that directory are numbered based
on their rank, i.e. cluster_1 refers to the top-ranked cluster. Information about the origin of these files can be found in that directory in the seletopclusts.txt file.
The simplest way to extract ranking information and the corresponding HADDOCK scores is to look at the X_caprieval directories (which is why it is a good idea to have it as the final module, and possibly as intermediate steps). This directory will always contain a capri_ss.tsv file, which contains the model names, rankings and statistics (score, iRMSD, Fnat, lRMSD, ilRMSD and dockq score). E.g.:
mmodel md5 caprieval_rank score irmsd fnat lrmsd ilrmsd dockq cluster-id cluster-ranking model-cluster-ranking air angles bonds bsa cdih coup dani desolv dihe elec improper rdcs rg total vdw vean xpcs ../6_emref/emref_11.pdb - 1 -151.136 1.261 0.741 2.673 2.192 0.746 2 1 1 79.990 0.000 0.000 2072.710 0.000 0.000 0.000 9.960 0.000 -598.859 0.000 0.000 0.000 -568.192 -49.323 0.000 0.000 ../6_emref/emref_15.pdb - 2 -137.252 1.237 0.845 2.713 2.253 0.783 2 1 2 83.274 0.000 0.000 2058.800 0.000 0.000 0.000 12.576 0.000 -584.402 0.000 0.000 0.000 -542.402 -41.275 0.000 0.000 ../6_emref/emref_19.pdb - 3 -136.527 1.550 0.621 4.283 3.353 0.634 2 1 3 200.318 0.000 0.000 1879.180 0.000 0.000 0.000 11.023 0.000 -704.878 0.000 0.000 0.000 -531.166 -26.606 0.000 0.000 ../6_emref/emref_14.pdb - 4 -131.142 1.658 0.776 3.271 3.005 0.699 2 1 4 163.724 0.000 0.000 2000.350 0.000 0.000 0.000 0.028 0.000 -449.205 0.000 0.000 0.000 -343.183 -57.702 0.000 0.000 ../6_emref/emref_1.pdb - 5 -128.501 14.936 0.069 22.861 21.984 0.067 3 2 1 159.850 0.000 0.000 1975.260 0.000 0.000 0.000 7.691 0.000 -451.593 0.000 0.000 0.000 -353.602 -61.859 0.000 0.000 ....
If clustering was performed prior to calling the caprieval module the capri_ss.tsv will also contain information about to which cluster the model belongs to and its ranking within the cluster as shown above.
The relevant statistics are:
- score: the HADDOCK score (arbitrary units)
- irmsd: the interface RMSD, calculated over the interfaces the molecules
- fnat: the fraction of native contacts
- lrmsd: the ligand RMSD, calculated on the ligand after fitting on the receptor (1st component)
- ilrmsd: the interface-ligand RMSD, calculated over the interface of the ligand after fitting on the interface of the receptor (more relevant for small ligands for example)
- dockq: the DockQ score, which is a combination of irmsd, lrmsd and fnat and provides a continuous scale between 1 (equal to reference) and 0
The iRMSD, lRMSD and Fnat metrics are the ones used in the blind protein-protein prediction experiment CAPRI (Critical PRediction of Interactions).
In CAPRI the quality of a model is defined as (for protein-protein complexes):
- acceptable model: i-RMSD < 4Å or l-RMSD<10Å and Fnat > 0.1
- medium quality model: i-RMSD < 2Å or l-RMSD<5Å and Fnat > 0.3
- high quality model: i-RMSD < 1Å or l-RMSD<1Å and Fnat > 0.5
What is based on this CAPRI criterion the quality of the best model listed above (emref_19.pdb)?
In case the caprieval module is called after a clustering step an additional file will be present in the directory: capri_clt.tsv.
This file contains the cluster ranking and score statistics, averaged over the minimum number of models defined for clustering
(4 by default), with their corresponding standard deviations. E.g.:
cluster_rank cluster_id n under_eval score score_std irmsd irmsd_std fnat fnat_std lrmsd lrmsd_std dockq dockq_std air air_std bsa bsa_std desolv desolv_std elec elec_std total total_std vdw vdw_std caprieval_rank 1 2 10 - -139.014 7.386 1.426 0.182 0.746 0.081 3.235 0.650 0.715 0.056 131.826 51.848 2002.760 76.340 8.397 4.920 -584.336 90.832 -496.236 89.379 -43.727 11.464 1 2 3 10 - -120.115 6.139 14.964 0.018 0.069 0.000 23.390 0.342 0.065 0.001 189.120 18.758 1998.883 56.075 4.601 5.111 -426.788 71.303 -295.939 64.795 -58.270 8.018 2 3 1 19 - -86.814 2.027 8.747 0.451 0.112 0.019 16.725 0.548 0.115 0.010 203.898 11.457 1554.495 32.501 7.527 1.994 -355.098 23.298 -194.910 27.573 -43.710 4.911 3 ...
In this file you find the cluster rank, the cluster ID (which is related to the size of the cluster, 1 being always the largest cluster), the number of models (n) in the cluster and the corresponding statistics (averages + standard deviations). The corresponding cluster PDB files will be found in the processing X_seletopclusts directory.
Analysis scenario 1: Paratope - antigen surface
Let us now analyze the docking results for this scenario. Use for that either your own run or a pre-calculated run provided in the runs directory (note that to save space only partial data have been kept in this pre-calculated runs, but all relevant information for this tutorial is available).
First of all let us check the final cluster statistics.
Inspect the capri_clt.tsv file
View the pre-calculated 9_caprieval/capri_clt.tsv file expand_more
cluster_rank cluster_id n under_eval score score_std irmsd irmsd_std fnat fnat_std lrmsd lrmsd_std dockq dockq_std air air_std bsa bsa_std desolv desolv_std elec elec_std total total_std vdw vdw_std caprieval_rank 1 12 20 - -148.831 5.410 1.678 0.214 0.733 0.106 3.865 0.862 0.669 0.076 185.424 46.938 2111.405 29.031 7.232 1.046 -570.066 22.622 -445.234 30.130 -60.592 5.236 1 2 18 18 - -123.766 3.115 13.094 0.125 0.000 0.000 21.834 0.146 0.048 0.001 183.704 11.225 2181.110 90.094 -10.254 2.067 -332.751 46.979 -214.379 31.846 -65.332 7.781 2 3 88 10 - -123.360 3.041 9.176 0.141 0.017 0.000 21.413 0.684 0.060 0.003 121.738 16.249 1813.925 34.884 -5.384 0.512 -436.619 11.830 -357.708 16.713 -42.827 3.868 3 4 13 20 - -118.282 5.208 10.944 0.299 0.120 0.021 21.415 0.619 0.092 0.006 152.420 10.986 1808.007 32.866 6.465 1.325 -496.468 28.628 -384.743 24.947 -40.696 2.465 4 5 89 10 - -116.454 3.801 14.020 0.134 0.017 0.000 24.744 0.187 0.045 0.001 195.446 27.781 1889.682 79.773 -4.616 1.591 -417.563 20.307 -269.986 30.222 -47.870 1.270 5 6 61 10 - -115.229 3.326 5.378 0.020 0.069 0.012 16.802 0.629 0.115 0.005 88.131 9.931 1852.945 23.752 6.616 0.785 -369.303 8.252 -337.969 11.465 -56.798 1.243 6 7 3 27 - -114.186 5.971 13.496 0.080 0.000 0.000 20.665 0.102 0.052 0.001 165.852 1.993 1707.362 39.298 -3.782 2.991 -376.041 22.069 -261.970 27.164 -51.781 5.373 7 8 72 10 - -112.872 6.827 13.981 0.020 0.000 0.000 21.801 0.126 0.048 0.000 132.974 16.434 1966.793 52.013 2.544 3.066 -294.085 43.518 -231.007 42.693 -69.896 9.485 8 9 1 36 - -109.409 4.762 14.617 0.071 0.000 0.000 23.183 0.063 0.043 0.000 197.155 20.227 1744.597 41.866 2.528 2.065 -328.410 33.521 -197.225 28.906 -65.970 1.565 9 10 17 18 - -108.195 7.362 11.031 0.082 0.000 0.000 20.012 0.260 0.057 0.001 164.234 10.186 1831.495 37.648 1.541 1.670 -396.469 47.982 -279.100 40.077 -46.865 5.102 10 11 96 10 - -107.334 2.166 10.667 0.151 0.000 0.000 21.692 0.437 0.051 0.002 142.746 7.402 1610.415 71.508 -1.450 3.091 -388.339 21.616 -288.084 14.372 -42.491 6.894 11 12 14 20 - -107.155 1.167 13.907 0.198 0.000 0.000 23.257 0.230 0.043 0.001 177.685 34.304 1817.573 49.504 -3.932 4.818 -359.962 72.737 -231.276 34.880 -48.999 7.524 12 13 58 10 - -105.459 2.853 9.418 0.041 0.017 0.000 14.704 0.253 0.098 0.002 142.162 20.088 1801.787 41.822 7.304 1.091 -390.603 6.402 -297.299 14.909 -48.858 1.289 13 14 7 22 - -104.950 8.949 12.591 0.206 0.000 0.000 21.517 0.421 0.050 0.002 137.010 17.810 1981.173 62.496 3.391 2.312 -294.790 53.286 -220.864 60.327 -63.084 12.713 14 15 110 8 - -104.523 5.407 15.786 0.141 0.000 0.000 24.742 0.292 0.038 0.001 188.247 28.369 1656.015 29.305 -7.098 2.026 -309.368 15.169 -175.498 17.510 -54.376 4.423 15 16 90 10 - -102.191 10.542 14.905 0.036 0.060 0.009 23.103 0.131 0.064 0.003 216.193 11.357 1942.820 85.100 5.473 2.317 -341.726 40.261 -186.471 38.069 -60.938 6.555 16 17 104 9 - -102.002 3.200 14.681 0.078 0.095 0.009 23.567 0.190 0.074 0.003 282.735 23.431 1944.375 30.920 5.480 0.963 -406.682 30.081 -178.366 9.480 -54.419 6.790 17 18 100 10 - -101.698 3.868 14.309 0.064 0.000 0.000 23.266 0.038 0.043 0.000 199.056 7.430 1988.773 23.017 -8.379 2.438 -240.464 33.134 -106.540 25.499 -65.132 4.179 18 19 98 10 - -100.603 4.480 12.350 0.118 0.000 0.000 21.122 0.363 0.051 0.001 252.315 14.795 1677.152 43.166 -3.298 0.773 -394.031 29.076 -185.446 16.087 -43.730 1.316 19 20 102 10 - -100.156 1.566 13.879 0.194 0.000 0.000 22.984 0.407 0.044 0.001 251.103 18.039 1770.800 64.193 -11.348 2.940 -282.111 7.081 -88.504 22.525 -57.496 2.031 20 21 16 19 - -100.048 2.675 12.712 0.077 0.000 0.000 21.116 0.748 0.051 0.003 141.121 20.656 1614.205 84.277 -7.610 2.379 -245.708 28.106 -161.995 21.053 -57.408 1.913 21 22 95 10 - -97.056 5.290 12.727 0.079 0.000 0.000 20.681 0.123 0.053 0.000 174.836 11.509 1808.197 27.762 7.899 2.831 -370.697 37.713 -244.160 41.611 -48.299 8.029 22 23 40 10 - -96.143 7.294 3.996 0.063 0.151 0.023 7.960 0.413 0.269 0.007 268.064 6.044 1733.595 64.045 5.918 1.741 -440.012 18.438 -212.812 23.620 -40.865 2.978 23 24 87 10 - -95.919 10.319 10.335 0.290 0.073 0.026 18.886 0.434 0.087 0.011 214.010 12.675 1786.825 65.807 -0.359 4.436 -345.955 25.147 -179.715 31.282 -47.770 4.496 24 25 29 13 - -94.903 5.148 11.976 0.456 0.000 0.000 20.189 0.481 0.056 0.002 180.302 16.905 1590.420 71.694 3.421 0.674 -407.384 36.274 -261.960 42.426 -34.878 4.826 25 26 82 10 - -94.568 1.367 13.254 0.087 0.021 0.007 23.375 0.213 0.050 0.002 139.468 19.278 1733.650 35.788 -7.849 1.524 -244.905 20.819 -157.122 27.990 -51.684 5.303 26 27 74 10 - -93.734 3.985 11.956 0.081 0.099 0.007 22.498 0.236 0.080 0.002 301.590 4.206 1764.012 79.875 -3.076 3.370 -299.142 56.102 -58.541 44.764 -60.989 9.410 27 28 19 17 - -92.956 3.507 13.908 0.268 0.026 0.015 23.921 0.385 0.050 0.004 266.721 14.416 1827.332 46.565 -0.139 2.193 -381.233 53.830 -157.755 45.492 -43.242 7.955 28 29 122 6 - -92.745 8.304 12.279 0.037 0.000 0.000 19.752 0.060 0.057 0.000 181.589 15.741 1752.342 47.374 1.028 1.586 -279.507 47.440 -153.948 58.429 -56.030 3.553 29 30 6 22 - -90.730 14.656 15.634 0.186 0.000 0.000 24.460 0.283 0.039 0.001 184.504 30.414 1646.735 13.700 -4.965 3.284 -279.679 35.172 -143.454 66.675 -48.279 4.415 30 31 9 20 - -90.251 2.575 13.154 0.202 0.017 0.000 20.607 0.234 0.058 0.001 245.319 26.351 1504.862 38.200 10.189 2.033 -416.678 30.459 -212.996 51.332 -41.636 4.161 31 32 22 16 - -90.038 7.776 13.627 0.190 0.021 0.014 24.214 0.496 0.048 0.006 184.562 6.921 1689.253 49.205 -3.136 2.159 -268.492 14.412 -135.590 22.903 -51.660 5.142 32 33 26 14 - -89.241 3.176 12.877 0.056 0.073 0.014 20.812 0.219 0.077 0.005 219.898 7.800 1397.388 66.657 9.547 1.503 -442.622 29.172 -254.977 24.167 -32.253 2.642 33 34 115 7 - -88.870 18.331 12.362 0.132 0.000 0.000 18.819 0.127 0.061 0.001 204.335 46.807 1699.523 139.984 12.768 1.118 -465.403 38.996 -290.059 88.987 -28.991 5.403 34 35 31 13 - -88.274 9.696 11.822 0.027 0.000 0.000 20.745 0.055 0.053 0.000 212.259 7.756 1703.915 75.126 7.349 1.187 -401.980 29.718 -226.174 34.586 -36.453 5.963 35 36 51 10 - -88.060 5.613 14.394 0.033 0.013 0.007 23.261 0.216 0.047 0.003 186.626 10.473 1530.995 13.755 -0.823 1.396 -285.016 40.961 -147.287 46.363 -48.896 3.714 36 37 4 27 - -87.381 3.159 14.366 0.075 0.000 0.000 23.345 0.143 0.043 0.000 262.042 8.675 1685.735 33.973 2.679 1.701 -375.458 19.104 -154.588 19.121 -41.172 3.024 37 38 66 10 - -86.618 5.301 14.360 0.065 0.065 0.007 22.073 0.117 0.068 0.002 175.771 18.244 1654.713 31.971 9.575 0.751 -391.041 27.344 -250.832 30.637 -35.561 2.215 38 39 105 9 - -86.351 7.447 12.441 0.119 0.000 0.000 21.061 0.886 0.052 0.003 203.393 38.498 1621.940 67.036 11.485 4.238 -397.087 49.285 -232.452 34.907 -38.758 6.513 39 40 2 28 - -85.386 3.721 8.292 0.100 0.060 0.009 14.033 0.238 0.120 0.004 223.683 20.263 1444.425 18.443 16.980 1.268 -531.053 52.923 -325.894 45.805 -18.524 8.161 40 41 99 10 - -85.318 3.371 14.167 0.142 0.000 0.000 23.073 0.125 0.044 0.000 210.252 30.361 1688.745 36.455 -3.802 1.262 -232.285 17.646 -78.117 29.587 -56.084 2.159 41 42 103 10 - -84.777 7.347 9.713 0.045 0.000 0.000 15.319 0.158 0.086 0.001 211.814 17.902 1762.062 62.020 -2.237 1.474 -302.213 19.881 -133.678 10.735 -43.278 8.354 42 43 11 20 - -84.755 3.002 10.202 0.038 0.000 0.000 16.040 0.210 0.080 0.001 242.024 11.938 1664.300 32.341 -1.048 2.058 -320.478 20.571 -122.268 20.568 -43.814 3.539 43 44 27 14 - -84.385 4.142 14.452 0.099 0.000 0.000 22.747 0.072 0.044 0.001 192.791 15.745 1680.112 60.521 8.681 0.414 -322.106 22.136 -177.239 23.588 -47.924 4.456 44 45 30 13 - -83.349 7.710 12.527 0.328 0.000 0.000 20.534 1.002 0.054 0.004 205.630 34.703 1630.215 82.132 0.730 2.859 -288.909 10.434 -130.138 41.408 -46.861 4.465 45 46 15 19 - -82.368 3.129 13.418 0.325 0.043 0.009 23.280 0.386 0.058 0.004 242.751 6.286 1658.195 38.410 5.431 0.414 -341.193 32.419 -142.278 23.070 -43.836 6.151 46 47 20 16 - -81.607 6.919 12.495 0.107 0.000 0.000 19.252 0.363 0.059 0.002 266.161 42.181 1672.205 55.410 5.343 4.413 -414.589 26.369 -179.076 49.862 -30.648 5.816 47 48 76 10 - -81.449 9.534 13.188 0.037 0.000 0.000 21.421 0.074 0.050 0.001 218.734 15.090 1736.692 89.208 -0.001 1.199 -290.595 36.010 -117.063 50.613 -45.203 3.614 48 49 8 20 - -81.182 4.279 10.455 0.122 0.000 0.000 16.979 0.225 0.073 0.002 202.172 4.326 1751.410 32.215 6.297 1.591 -296.855 38.493 -143.008 36.221 -48.325 6.151 49 50 83 10 - -80.925 4.370 12.827 0.095 0.000 0.000 18.830 0.175 0.061 0.001 178.048 13.548 1484.358 38.444 5.855 0.509 -387.956 12.917 -236.901 11.192 -26.994 3.744 50 51 80 10 - -80.920 1.233 8.605 0.110 0.000 0.000 14.204 0.254 0.098 0.003 263.125 9.132 1680.088 44.302 -2.533 1.044 -276.380 9.676 -62.678 11.913 -49.423 2.206 51 52 65 10 - -80.630 3.310 14.620 0.066 0.000 0.000 22.569 0.112 0.045 0.000 288.688 2.621 1667.402 19.562 6.148 0.292 -359.050 7.320 -114.200 9.850 -43.837 2.804 52 53 78 10 - -80.553 1.319 15.253 0.064 0.000 0.000 23.967 0.193 0.041 0.001 243.820 10.141 1722.265 32.414 -6.757 0.875 -233.628 32.754 -41.260 21.926 -51.452 6.462 53 54 91 10 - -80.434 7.690 12.606 0.433 0.065 0.007 22.027 0.766 0.070 0.005 239.985 31.342 1715.950 113.990 -2.244 1.763 -276.599 35.568 -83.483 44.904 -46.869 5.835 54 55 86 10 - -79.938 1.932 14.133 0.054 0.000 0.000 21.594 0.090 0.049 0.001 234.653 13.341 1560.172 37.779 -2.434 3.230 -216.869 17.452 -39.812 24.206 -57.595 0.798 55 56 94 10 - -79.785 3.074 14.163 0.044 0.000 0.000 23.755 0.224 0.042 0.001 233.620 10.459 1617.775 27.712 -4.985 3.008 -246.368 23.556 -61.636 15.735 -48.888 3.624 56 57 57 10 - -79.647 3.136 14.334 0.035 0.000 0.000 22.584 0.139 0.045 0.001 206.786 21.758 1752.880 43.951 4.484 1.474 -292.769 26.191 -132.238 35.347 -46.255 2.074 57 58 109 8 - -79.637 4.090 14.374 0.029 0.000 0.000 23.226 0.171 0.043 0.001 179.447 18.968 1587.280 48.041 -6.736 4.312 -216.970 21.146 -84.975 34.722 -47.452 4.918 58 59 125 4 - -79.181 3.093 13.707 0.110 0.013 0.007 25.049 0.264 0.043 0.002 208.704 5.337 1603.477 18.923 0.803 3.084 -320.220 17.996 -148.327 16.357 -36.811 2.829 59 60 75 10 - -79.050 2.188 9.582 0.072 0.013 0.007 17.607 0.404 0.075 0.002 255.051 11.542 1487.710 19.121 -3.626 3.331 -272.006 25.775 -63.483 15.928 -46.528 1.228 60 61 21 16 - -78.910 7.107 12.204 0.791 0.000 0.000 19.571 0.565 0.058 0.003 265.529 23.762 1628.423 100.079 -7.391 2.450 -259.371 19.026 -40.040 31.465 -46.198 2.505 61 62 119 6 - -78.891 12.708 12.225 0.073 0.000 0.000 21.918 0.277 0.049 0.001 183.873 60.583 1612.245 43.225 5.173 2.252 -342.645 40.522 -192.694 94.271 -33.921 1.601 62 63 32 12 - -78.111 4.787 11.640 0.490 0.030 0.007 19.381 0.419 0.070 0.005 224.618 24.572 1458.675 59.540 12.585 2.659 -404.922 39.771 -212.478 43.741 -32.174 7.745 63 64 93 10 - -75.558 0.893 15.617 0.035 0.000 0.000 25.553 0.142 0.036 0.001 234.040 18.302 1612.077 87.261 -2.881 1.880 -222.506 13.334 -40.046 22.117 -51.580 3.451 64 65 53 10 - -74.878 0.925 11.095 0.055 0.000 0.000 19.669 0.309 0.058 0.001 217.684 13.625 1737.645 54.714 4.811 2.265 -267.514 39.563 -97.784 28.401 -47.954 8.106 65 66 50 10 - -74.229 3.215 9.398 0.118 0.000 0.000 15.157 0.226 0.088 0.002 201.585 13.616 1307.077 34.282 7.107 1.138 -346.429 18.226 -177.052 16.240 -32.209 2.692 66 67 46 10 - -74.057 6.696 13.393 0.171 0.038 0.008 20.998 0.234 0.064 0.004 182.613 28.046 1532.910 44.960 11.778 4.762 -283.146 29.545 -148.000 30.970 -47.467 2.189 67 68 10 20 - -73.940 3.036 10.540 0.046 0.017 0.000 19.176 0.153 0.067 0.001 356.795 15.142 1492.230 74.353 15.509 2.170 -510.698 9.877 -176.892 19.108 -22.989 0.857 68 69 44 10 - -73.811 2.120 13.513 0.025 0.000 0.000 20.546 0.111 0.052 0.001 210.162 18.014 1370.822 23.324 5.688 1.348 -373.221 16.893 -188.930 22.084 -25.871 3.664 69 70 101 10 - -73.605 5.664 7.585 0.291 0.194 0.007 15.971 0.612 0.151 0.003 239.400 28.980 1437.820 17.631 2.496 1.252 -306.286 30.593 -105.669 8.236 -38.784 7.589 70 71 73 10 - -73.330 14.683 8.421 0.080 0.142 0.022 16.234 0.195 0.129 0.007 291.068 13.141 1524.905 74.286 7.236 1.570 -318.544 28.529 -73.439 41.719 -45.964 8.000 71 72 79 10 - -72.710 2.560 11.891 0.070 0.017 0.000 21.817 0.101 0.055 0.000 267.791 10.125 1643.050 30.536 -1.153 0.712 -316.054 21.622 -83.389 26.219 -35.125 3.184 72 73 108 8 - -72.053 6.427 14.141 0.080 0.000 0.000 22.606 0.088 0.045 0.000 274.130 28.215 1575.818 26.120 2.867 4.129 -353.149 37.289 -110.722 50.901 -31.703 6.123 73 74 116 7 - -71.931 3.431 14.263 0.020 0.021 0.007 21.881 0.092 0.055 0.002 239.220 23.289 1488.585 51.307 11.289 2.327 -337.511 20.455 -137.931 34.222 -39.639 2.696 74 75 23 15 - -71.317 1.735 9.651 0.111 0.000 0.000 15.522 0.401 0.085 0.003 194.466 13.162 1484.050 42.048 9.548 1.288 -290.001 20.663 -137.847 15.853 -42.312 1.866 75 76 24 15 - -71.030 2.953 16.556 0.115 0.000 0.000 28.355 0.305 0.030 0.000 205.405 8.091 1334.508 11.170 -5.633 2.051 -183.413 17.299 -27.264 20.045 -49.255 2.861 76 77 28 13 - -70.176 3.460 14.159 0.213 0.004 0.007 22.016 0.254 0.048 0.003 212.614 35.492 1491.645 40.439 8.647 0.432 -294.032 36.700 -122.695 8.604 -41.277 2.477 77 78 37 11 - -69.964 1.337 15.376 0.133 0.000 0.000 25.078 0.326 0.037 0.001 271.813 14.529 1713.650 51.673 -7.231 2.128 -241.582 17.736 -11.367 27.829 -41.599 3.838 78 79 123 5 - -69.304 4.503 16.450 0.148 0.000 0.000 27.833 0.537 0.031 0.001 210.556 19.322 1326.200 45.711 -5.965 1.162 -161.157 6.948 -2.764 25.378 -52.163 3.012 79 80 106 9 - -67.503 6.037 12.789 0.289 0.026 0.015 23.061 1.336 0.053 0.002 296.781 34.983 1620.858 52.591 5.560 2.969 -348.713 38.348 -84.930 63.453 -32.998 4.669 80 81 120 6 - -67.302 2.532 14.358 0.041 0.000 0.000 22.837 0.023 0.044 0.000 271.706 12.518 1634.723 24.273 0.998 1.097 -227.589 9.829 -5.836 14.119 -49.953 3.620 81 82 55 10 - -67.097 3.840 6.036 0.861 0.090 0.014 12.039 0.749 0.162 0.019 384.023 42.496 1531.295 87.955 3.794 4.479 -454.914 59.765 -89.202 76.199 -18.311 9.697 82 83 124 4 - -66.655 5.062 6.249 0.264 0.224 0.012 11.025 0.671 0.217 0.008 235.183 27.050 1650.928 104.661 12.126 3.442 -328.671 31.748 -130.053 21.804 -36.565 3.933 83 84 34 11 - -66.442 5.053 14.336 0.479 0.056 0.023 24.830 1.011 0.057 0.010 253.232 30.608 1472.758 125.167 2.441 1.679 -290.510 38.258 -73.383 33.664 -36.105 2.888 84 85 38 10 - -64.966 3.389 12.351 0.042 0.000 0.000 18.220 0.062 0.065 0.001 237.737 22.406 1463.210 47.096 18.877 2.622 -395.482 9.668 -186.266 30.185 -28.521 1.362 85 86 62 10 - -64.964 5.998 7.746 0.112 0.004 0.007 15.178 0.486 0.093 0.004 271.487 9.093 1577.678 76.023 -0.556 4.196 -206.951 36.880 14.369 36.913 -50.167 1.787 86 87 25 15 - -64.334 4.335 13.027 0.411 0.021 0.007 23.541 0.557 0.050 0.001 185.122 8.359 1583.560 19.045 -1.219 6.525 -176.576 111.800 -37.766 99.230 -46.312 12.209 87 88 42 10 - -62.875 14.148 14.485 0.024 0.000 0.000 23.143 0.209 0.043 0.001 179.610 11.087 1721.772 71.776 12.319 3.484 -243.120 35.868 -108.042 47.241 -44.532 3.820 88 89 84 10 - -62.085 1.306 14.514 0.132 0.000 0.000 22.149 0.316 0.046 0.001 296.997 14.696 1383.428 30.064 1.898 3.669 -292.144 12.479 -30.401 25.823 -35.254 1.893 89 90 121 6 - -61.957 4.116 12.331 0.311 0.000 0.000 19.451 0.605 0.058 0.003 270.992 23.909 1274.112 82.006 4.029 2.380 -266.295 41.053 -35.130 24.369 -39.827 4.542 90 91 36 11 - -61.811 2.141 14.445 0.058 0.000 0.000 22.627 0.070 0.045 0.000 270.514 14.399 1609.382 28.876 1.751 1.481 -254.673 33.427 -23.837 34.147 -39.679 5.666 91 92 77 10 - -61.079 5.725 5.780 0.082 0.039 0.015 10.799 0.259 0.162 0.009 240.534 37.298 1483.005 50.398 -0.002 2.077 -182.518 25.073 9.390 46.237 -48.626 2.883 92 93 117 6 - -60.777 11.533 9.801 0.191 0.013 0.007 21.006 0.640 0.059 0.004 246.636 8.427 1268.660 71.298 6.936 2.487 -314.050 22.326 -96.981 32.734 -29.567 6.294 93 94 85 10 - -60.209 2.297 11.213 0.218 0.000 0.000 18.816 0.542 0.062 0.003 381.891 10.325 1459.902 67.889 -2.759 1.863 -266.267 22.682 73.237 24.125 -42.386 2.780 94 95 126 4 - -59.397 3.161 13.514 0.088 0.000 0.000 20.613 0.206 0.052 0.001 340.899 11.341 1457.237 38.500 0.742 1.761 -285.606 3.678 18.186 8.403 -37.107 1.557 95 96 63 10 - -59.291 7.296 9.014 0.111 0.000 0.000 16.822 0.663 0.077 0.005 280.676 22.422 1318.048 29.172 9.234 1.737 -325.262 28.578 -76.127 49.934 -31.541 1.854 96 97 70 10 - -58.877 4.462 13.014 0.056 0.000 0.000 22.464 0.254 0.046 0.001 228.543 28.692 1422.508 65.438 -4.012 3.320 -200.927 16.946 -9.918 31.989 -37.534 1.424 97 98 45 10 - -58.029 6.480 7.814 0.140 0.017 0.000 13.251 0.317 0.115 0.004 229.389 29.836 1404.900 46.790 11.103 1.955 -327.900 39.785 -125.001 51.497 -26.490 2.094 98 99 68 10 - -55.807 3.727 16.510 0.066 0.000 0.000 25.624 0.263 0.036 0.001 318.869 16.264 1213.652 9.474 -5.589 2.224 -229.506 11.490 53.160 7.966 -36.203 3.035 99 100 67 10 - -55.715 3.802 14.121 0.078 0.073 0.007 23.021 0.127 0.068 0.003 364.598 7.533 1424.082 38.150 0.216 3.221 -301.127 9.515 31.305 11.925 -32.166 2.426 100 101 43 10 - -55.357 4.538 13.771 0.174 0.000 0.000 22.382 0.222 0.046 0.001 315.525 17.911 1224.170 95.586 15.578 3.930 -449.307 38.562 -146.408 51.664 -12.626 5.604 101 102 60 10 - -55.224 0.578 14.483 0.242 0.000 0.000 26.049 0.668 0.036 0.002 237.155 10.847 1474.113 27.846 0.259 1.804 -152.957 35.644 35.591 28.921 -48.607 4.912 102 103 59 10 - -55.141 2.610 14.717 0.093 0.034 0.000 23.704 0.289 0.053 0.001 298.384 26.262 1406.250 66.647 9.341 3.393 -316.841 23.707 -49.410 30.705 -30.952 4.042 103 104 112 7 - -54.921 9.461 10.685 0.208 0.073 0.026 18.506 0.476 0.089 0.007 219.840 44.971 1521.922 81.424 5.709 7.046 -214.847 15.424 -34.651 49.783 -39.644 4.737 104 105 5 22 - -54.314 4.331 12.385 0.086 0.021 0.014 22.595 0.342 0.053 0.006 233.002 17.524 1358.430 35.130 1.471 0.185 -207.591 22.952 -12.155 32.463 -37.567 1.570 105 106 52 10 - -53.491 15.207 12.353 0.103 0.000 0.000 22.051 0.367 0.048 0.001 233.007 31.498 1414.820 102.212 3.750 1.618 -249.119 20.721 -46.830 57.818 -30.718 7.272 106 107 111 7 - -53.239 5.226 13.791 0.212 0.000 0.000 23.428 0.626 0.043 0.002 268.166 12.080 1414.135 56.300 7.739 1.257 -222.832 3.164 2.106 14.206 -43.228 4.768 107 108 54 10 - -52.971 3.488 14.200 0.033 0.000 0.000 23.847 0.087 0.041 0.000 334.087 9.226 1546.130 36.750 -6.005 1.905 -190.261 19.194 101.503 17.352 -42.322 4.900 108 109 56 10 - -51.490 5.020 13.521 0.052 0.000 0.000 22.416 0.243 0.046 0.001 293.306 19.777 1477.102 25.522 5.609 1.461 -279.596 12.796 -16.800 25.540 -30.510 5.347 109 110 118 6 - -51.117 4.561 12.365 0.051 0.000 0.000 23.714 0.346 0.043 0.001 278.889 18.649 1432.265 9.470 0.370 2.751 -214.671 17.337 27.776 25.570 -36.442 3.072 110 111 107 9 - -49.501 5.059 14.835 0.038 0.000 0.000 23.410 0.057 0.042 0.000 344.941 19.284 1343.577 12.807 -3.153 1.679 -264.398 20.388 52.580 29.967 -27.963 9.609 111 112 35 11 - -49.340 2.447 11.317 0.928 0.039 0.015 20.295 1.572 0.069 0.011 235.385 37.942 1409.605 87.748 4.069 3.360 -185.705 44.350 9.873 43.861 -39.807 8.325 112 113 33 12 - -46.737 4.308 11.174 0.816 0.000 0.000 19.641 1.416 0.059 0.007 310.128 20.042 1238.068 110.488 4.568 2.574 -256.976 22.111 22.230 37.127 -30.923 2.384 113 114 113 7 - -45.800 5.982 10.348 0.124 0.000 0.000 18.316 0.481 0.066 0.003 282.571 18.197 1311.367 56.380 4.791 1.847 -211.064 18.902 34.872 19.595 -36.635 3.931 114 115 81 10 - -45.354 6.929 16.636 0.096 0.000 0.000 25.863 0.726 0.035 0.002 308.236 11.719 1275.400 52.716 -5.692 4.714 -181.522 49.756 92.533 51.322 -34.181 9.503 115 116 49 10 - -44.705 1.959 10.852 0.035 0.000 0.000 16.845 0.062 0.074 0.000 358.788 5.112 1341.040 72.642 10.412 2.121 -347.849 36.059 -10.488 33.632 -21.427 6.467 116 117 39 10 - -44.261 4.620 14.087 0.056 0.000 0.000 22.835 0.013 0.044 0.000 295.495 17.162 1234.227 27.363 4.174 3.430 -210.269 16.733 49.294 18.637 -35.931 4.941 117 118 92 10 - -44.053 1.106 15.813 0.128 0.000 0.000 25.745 0.368 0.036 0.001 283.916 13.486 1275.445 30.036 -6.639 1.857 -143.568 20.594 103.256 10.722 -37.092 1.745 118 119 114 7 - -43.996 7.676 13.036 0.151 0.000 0.000 21.041 0.248 0.051 0.001 318.293 22.689 1397.472 69.100 6.502 2.294 -242.837 58.413 41.697 35.569 -33.760 4.092 119 120 127 4 - -42.868 12.804 10.782 0.266 0.021 0.007 18.935 0.277 0.070 0.003 378.484 32.539 1279.013 79.482 -2.333 3.174 -249.324 69.688 100.641 96.319 -28.519 2.196 120 121 97 10 - -41.988 1.493 15.101 0.025 0.000 0.000 23.745 0.034 0.041 0.000 301.125 3.112 1269.653 33.464 -8.743 1.470 -129.712 11.741 133.997 11.234 -37.416 1.471 121 122 71 10 - -41.763 0.892 8.507 0.097 0.039 0.015 14.685 0.147 0.107 0.006 239.057 9.121 1327.050 24.875 8.577 4.145 -218.493 30.755 -9.983 30.699 -30.547 4.870 122 123 47 10 - -36.220 3.928 15.277 0.106 0.000 0.000 23.010 0.110 0.043 0.000 284.950 8.282 1175.388 69.795 5.948 1.847 -213.173 34.270 43.748 38.868 -28.029 3.546 123 124 41 10 - -32.454 10.820 12.104 0.204 0.000 0.000 20.116 0.705 0.056 0.003 396.786 30.865 1066.531 89.515 12.815 3.725 -377.880 29.248 9.535 54.759 -9.372 2.922 124 125 64 10 - -27.162 1.992 10.301 0.345 0.000 0.000 18.657 0.861 0.065 0.005 402.122 49.749 1030.695 25.469 4.338 0.861 -257.608 45.825 124.323 22.168 -20.191 4.685 125 126 48 10 - -14.746 4.336 10.121 0.049 0.000 0.000 18.586 0.361 0.065 0.002 357.317 19.257 1018.395 44.464 1.525 1.784 -147.322 10.412 187.457 30.279 -22.539 2.476 126 127 69 10 - -13.047 2.110 13.381 0.036 0.000 0.000 23.537 0.088 0.043 0.000 326.021 21.144 1056.715 43.823 -2.112 1.084 -98.899 7.148 203.364 15.655 -23.757 1.618 127
How many clusters are generated?
Since for this tutorial we have at hand the crystal structure of the complex, we provided it as reference to the caprieval modules.
This means that the iRMSD, lRMSD, Fnat and DockQ statistics report on the quality of the docked model compared to the reference crystal structure.
How many clusters of acceptable or better quality have been generate according to CAPRI criteria?
What is the rank of the best cluster generated?
What is the rank of the first acceptable of better cluster generated?
In this run we also had a caprieval after the clustering of the rigid body models (step 4 of our workflow).
Inspect the corresponding capri_clt.tsv file
View the pre-calculated 4_caprieval/capri_clt.tsv file expand_more
cluster_rank cluster_id n under_eval score score_std irmsd irmsd_std fnat fnat_std lrmsd lrmsd_std dockq dockq_std air air_std bsa bsa_std desolv desolv_std elec elec_std total total_std vdw vdw_std caprieval_rank 1 48 10 - -13.844 0.900 13.404 0.035 0.000 0.000 22.237 0.123 0.046 0.001 1166.617 117.075 1315.115 40.932 -9.803 2.749 -3.493 0.991 1256.845 137.335 93.721 19.507 1 9 138 10 - -10.454 0.674 13.607 0.000 0.000 0.000 22.064 0.000 0.047 0.000 1204.100 0.000 1665.775 24.438 -3.712 0.820 -2.350 0.000 1224.210 0.000 22.460 0.002 2 3 11 10 - -10.412 0.432 15.857 0.000 0.000 0.000 24.564 0.000 0.039 0.000 1384.043 0.004 1245.633 13.154 -6.563 0.429 -5.648 0.000 1419.910 0.000 41.513 0.001 3 2 15 10 - -10.340 0.286 16.017 0.000 0.000 0.000 24.570 0.000 0.039 0.000 1333.983 0.004 1253.492 15.726 -1.585 0.327 -9.873 0.000 1355.403 0.004 31.294 0.002 4 4 106 10 - -9.829 0.222 15.391 0.000 0.000 0.000 24.525 0.000 0.039 0.000 1552.235 0.005 1383.528 17.921 -7.734 0.159 -4.185 0.000 1588.340 0.000 40.293 0.003 5 6 69 10 - -9.533 1.575 12.950 0.269 0.000 0.000 20.490 1.095 0.054 0.005 1276.435 67.292 1199.227 109.102 -8.069 0.667 -2.824 1.663 1332.377 61.750 58.763 7.369 6 5 83 10 - -9.012 0.282 14.254 0.000 0.000 0.000 22.921 0.000 0.044 0.000 1276.120 0.010 1183.360 18.970 -3.152 0.213 -7.525 0.000 1342.325 0.005 73.727 0.006 7 7 80 10 - -7.775 0.494 9.909 0.113 0.000 0.000 15.681 0.333 0.083 0.002 1542.185 35.608 1324.515 18.563 -4.813 0.320 -5.803 0.471 1602.840 32.869 66.456 2.271 8 12 146 10 - -7.423 0.848 14.398 0.000 0.000 0.000 23.944 0.000 0.041 0.000 1442.685 0.005 1299.652 32.980 -7.305 1.130 -1.911 0.000 1476.980 0.000 36.202 0.001 9 8 103 10 - -7.333 0.221 14.981 0.000 0.000 0.000 24.008 0.000 0.040 0.000 1543.658 0.004 1030.420 14.645 -10.900 0.124 -2.262 0.000 1610.960 0.000 69.566 0.001 10 10 57 10 - -6.935 0.458 14.379 0.000 0.000 0.000 23.639 0.000 0.042 0.000 1222.643 0.004 1453.100 18.107 -6.100 0.353 0.439 0.000 1326.150 0.000 103.066 0.004 11 19 143 10 - -6.913 0.973 15.057 0.055 0.000 0.000 23.498 0.016 0.042 0.000 1637.182 34.931 1089.412 27.157 -8.432 1.560 -4.361 0.102 1673.073 22.235 40.253 12.796 12 11 46 10 - -6.612 0.137 7.774 0.000 0.138 0.000 16.369 0.000 0.129 0.000 1427.530 0.000 1264.045 12.113 -2.676 0.088 -6.756 0.000 1539.297 0.004 118.522 0.001 13 13 74 10 - -6.451 0.515 12.795 0.110 0.000 0.000 21.337 0.231 0.050 0.001 1227.858 0.583 1320.807 16.754 -3.158 0.556 -2.694 0.171 1258.178 3.958 33.012 4.713 14 14 40 10 - -6.057 0.570 14.552 0.000 0.000 0.000 23.108 0.000 0.043 0.000 1325.322 0.004 1317.838 17.495 -3.007 0.666 -3.439 0.000 1353.310 0.000 31.430 0.001 15 17 54 10 - -5.998 0.121 12.456 0.000 0.000 0.000 19.696 0.000 0.057 0.000 1314.395 0.005 1310.680 23.796 -1.208 0.317 -5.261 0.000 1352.630 0.000 43.495 0.001 16 15 32 10 - -5.964 0.425 14.596 0.115 0.000 0.000 23.358 0.122 0.043 0.000 1277.912 7.923 1285.055 82.743 -3.391 0.456 -2.900 0.806 1314.905 3.200 39.893 5.527 17 16 12 10 - -5.777 0.104 13.551 0.000 0.017 0.000 23.658 0.000 0.048 0.000 1198.952 0.008 1149.155 9.000 -1.300 0.161 -5.170 0.000 1213.340 0.000 19.559 0.004 18 18 124 10 - -5.691 0.215 14.454 0.000 0.017 0.000 23.355 0.000 0.048 0.000 1416.720 0.007 1374.565 18.449 -4.243 0.272 -2.310 0.000 1458.433 0.004 44.024 0.004 19 21 56 10 - -5.412 0.747 15.959 0.000 0.000 0.000 25.689 0.001 0.036 0.000 1217.487 0.004 1439.070 19.619 -0.762 0.765 -2.668 0.000 1238.170 0.000 23.352 0.001 20 29 104 10 - -5.375 0.124 13.872 0.000 0.000 0.000 20.781 0.000 0.052 0.000 1406.888 0.015 1020.282 14.806 -3.770 0.202 -6.285 0.000 1481.987 0.004 81.386 0.009 21 20 49 10 - -5.250 0.321 15.360 0.000 0.000 0.000 23.819 0.000 0.041 0.000 1494.370 0.000 1010.559 24.070 -8.385 0.381 -2.102 0.000 1532.178 0.004 39.910 0.001 22 23 14 10 - -4.989 1.157 10.910 0.000 0.000 0.000 21.035 0.000 0.053 0.000 1197.435 0.015 1289.438 22.539 -1.583 1.033 -2.975 0.000 1243.383 0.004 48.924 0.011 23 24 44 10 - -4.755 0.228 11.912 0.000 0.034 0.000 22.612 0.000 0.058 0.000 1538.758 0.004 1152.660 13.464 -4.545 0.280 -4.549 0.000 1582.030 0.000 47.828 0.000 24 25 29 10 - -4.750 0.679 10.824 0.420 0.009 0.009 18.404 1.004 0.068 0.006 1371.130 157.122 1214.263 97.267 -3.579 1.850 -3.541 1.647 1447.700 178.555 80.112 41.852 25 22 23 10 - -4.670 0.217 13.640 0.000 0.000 0.000 20.717 0.000 0.052 0.000 1074.330 0.000 1374.390 4.007 0.869 0.209 -2.729 0.000 1090.750 0.000 19.152 0.001 26 28 38 10 - -4.363 0.605 16.033 0.155 0.000 0.000 25.480 0.271 0.036 0.001 1238.952 29.106 1052.057 45.106 -7.738 1.761 1.048 2.035 1285.750 39.525 45.747 12.456 27 27 1 10 - -4.137 0.568 10.316 0.088 0.000 0.000 16.498 0.391 0.076 0.003 1721.757 67.381 1135.003 53.658 -4.618 0.422 -5.766 0.216 1754.023 66.472 38.026 0.691 28 26 27 10 - -4.112 0.152 12.983 0.000 0.000 0.000 20.773 0.000 0.052 0.000 1139.570 0.000 1462.320 16.198 1.793 0.279 -2.812 0.000 1150.210 0.000 13.452 0.001 29 30 61 10 - -4.099 0.842 13.370 0.239 0.000 0.000 21.815 0.084 0.048 0.000 1308.007 135.944 1550.715 205.819 1.005 1.959 -2.987 1.590 1336.082 149.353 31.061 14.996 30 37 112 10 - -3.676 0.381 14.796 0.000 0.000 0.000 22.998 0.000 0.043 0.000 1486.800 0.000 1227.990 15.606 -0.708 0.396 -6.135 0.000 1538.500 0.000 57.833 0.002 31 31 34 10 - -3.597 0.147 14.799 0.061 0.000 0.000 23.015 0.136 0.043 0.001 1310.543 23.128 1183.075 91.732 -0.950 0.684 -4.455 0.136 1359.398 1.033 53.309 21.961 32 32 7 10 - -3.508 0.513 16.858 0.000 0.000 0.000 28.409 0.000 0.030 0.000 1301.480 0.000 1196.672 8.578 -4.923 0.571 -0.218 0.000 1359.760 0.000 58.499 0.001 33 33 20 10 - -2.773 0.374 14.904 0.000 0.000 0.000 23.214 0.000 0.043 0.000 1183.130 0.000 1460.190 23.915 1.641 0.539 -1.872 0.000 1204.100 0.000 22.843 0.001 34 35 77 10 - -2.739 0.764 12.238 0.036 0.000 0.000 19.323 0.055 0.059 0.000 1282.035 90.578 1268.540 64.375 -0.585 2.814 -2.576 0.397 1308.220 104.985 28.759 14.014 35 42 42 10 - -2.495 1.064 9.577 0.000 0.017 0.000 21.186 0.000 0.060 0.000 1085.117 0.004 1410.815 38.489 0.948 0.957 -0.636 0.000 1129.460 0.000 44.976 0.002 36 40 62 10 - -2.017 0.480 14.651 0.000 0.000 0.000 22.953 0.000 0.044 0.000 1362.965 0.005 1379.763 20.658 2.498 0.488 -4.718 0.000 1395.325 0.005 37.078 0.003 37 34 64 10 - -2.009 0.327 12.646 0.167 0.065 0.007 21.928 0.363 0.070 0.004 1227.983 17.299 1275.485 30.604 -2.275 0.709 0.190 0.874 1283.332 19.239 55.160 2.813 38 39 105 10 - -1.975 0.713 11.651 0.000 0.086 0.000 20.866 0.000 0.082 0.000 1426.785 0.005 1445.892 18.713 -1.552 0.833 -0.564 0.000 1459.400 0.000 33.182 0.001 39 36 100 10 - -1.974 0.614 14.641 0.375 0.017 0.000 25.137 0.604 0.044 0.001 1613.605 50.415 1285.878 28.846 -1.852 1.404 -4.480 2.223 1717.162 105.853 108.035 57.663 40 56 88 10 - -1.877 1.153 14.595 0.000 0.017 0.000 22.930 0.000 0.050 0.000 1377.500 0.000 1256.900 19.112 1.216 1.144 -4.825 0.000 1425.230 0.000 52.558 0.001 41 41 36 10 - -1.834 0.548 13.132 0.000 0.000 0.000 21.975 0.000 0.048 0.000 972.241 0.007 1488.515 12.437 5.426 0.465 -2.704 0.000 1030.163 0.004 60.625 0.003 42 38 30 10 - -1.684 0.302 14.753 0.000 0.069 0.000 23.211 0.000 0.066 0.000 1193.767 0.018 1714.410 16.251 4.303 0.358 -0.954 0.000 1210.110 0.007 17.296 0.011 43 43 85 10 - -1.494 0.422 2.535 0.000 0.345 0.000 6.023 0.000 0.423 0.000 1955.515 0.005 1609.628 8.936 11.827 0.474 -17.319 0.000 1992.133 0.004 53.936 0.002 44 48 75 10 - -1.190 1.574 12.890 0.000 0.000 0.000 21.606 0.000 0.049 0.000 1678.058 0.004 1003.288 20.621 -3.349 1.741 -5.239 0.000 1737.880 0.000 65.063 0.003 45 44 4 10 - -1.162 0.159 13.134 0.000 0.017 0.000 20.540 0.000 0.059 0.000 1402.763 0.004 1128.918 30.713 4.675 0.392 -8.789 0.000 1415.280 0.000 21.304 0.001 46 45 17 10 - -1.158 0.437 14.586 0.000 0.017 0.000 22.061 0.000 0.052 0.000 1350.850 0.000 1109.115 12.543 4.974 0.472 -9.271 0.000 1413.800 0.000 72.221 0.002 47 46 127 10 - -1.143 0.190 14.426 0.000 0.000 0.000 22.311 0.000 0.046 0.000 1326.025 0.005 1255.963 21.347 -0.151 0.291 -2.092 0.000 1363.835 0.005 39.904 0.003 48 58 149 10 - -0.788 0.547 14.657 0.000 0.000 0.000 23.481 0.001 0.042 0.000 1230.210 0.012 1123.400 25.376 0.072 0.545 -2.759 0.000 1310.590 0.007 83.137 0.006 49 47 47 10 - -0.634 0.202 10.615 0.000 0.000 0.000 17.214 0.000 0.072 0.000 1582.995 0.005 1101.400 8.505 -3.618 0.282 -2.392 0.000 1636.595 0.005 55.990 0.002 50 50 65 10 - -0.544 0.694 14.396 0.000 0.000 0.000 21.711 0.000 0.048 0.000 1204.223 0.004 1317.295 29.407 1.424 0.855 -1.151 0.000 1234.443 0.004 31.369 0.004 51 49 123 10 - -0.413 0.261 14.733 0.000 0.000 0.000 22.393 0.000 0.045 0.000 1690.878 0.013 1054.225 25.599 -2.721 0.379 -4.661 0.000 1746.453 0.008 60.234 0.010 52 53 41 10 - -0.301 0.901 11.978 0.000 0.000 0.000 20.686 0.000 0.053 0.000 1281.405 0.005 1249.838 29.204 4.705 0.853 -6.289 0.001 1371.910 0.000 96.793 0.001 53 52 72 10 - 0.004 0.778 11.393 0.000 0.000 0.000 18.815 0.000 0.062 0.000 1841.592 0.004 1184.938 24.043 -2.198 0.990 -4.820 0.000 1882.420 0.000 45.649 0.002 54 55 60 10 - 0.009 0.555 12.540 0.000 0.000 0.000 22.058 0.000 0.048 0.000 1472.052 0.008 1173.470 32.950 1.109 0.517 -4.536 0.001 1512.588 0.004 45.071 0.002 55 51 33 10 - 0.107 0.243 13.624 0.000 0.000 0.000 22.164 0.000 0.047 0.000 1015.085 0.011 1247.485 25.589 6.940 0.203 -4.666 0.000 1026.035 0.005 15.620 0.008 56 64 107 10 - 0.205 0.370 10.381 0.000 0.017 0.000 18.922 0.000 0.069 0.000 1627.175 0.009 1123.535 23.337 -0.720 0.382 -4.857 0.000 1696.867 0.004 74.549 0.006 57 54 66 10 - 0.360 0.318 1.684 0.402 0.526 0.181 3.075 0.744 0.622 0.116 1597.793 284.803 1513.723 249.385 8.918 5.003 -10.031 0.661 1650.948 320.308 63.184 36.167 58 57 111 10 - 0.766 0.550 14.904 0.000 0.000 0.000 22.475 0.000 0.045 0.000 1626.950 0.007 1014.321 27.012 -1.440 0.342 -4.577 0.000 1688.060 0.000 65.685 0.004 59 59 55 10 - 0.858 0.540 13.865 0.000 0.017 0.000 23.838 0.000 0.047 0.000 1807.443 0.004 1378.845 3.558 8.995 0.538 -12.902 0.000 1842.455 0.005 47.919 0.003 60 62 147 10 - 0.956 0.701 15.581 0.054 0.000 0.000 24.005 0.203 0.041 0.001 1597.950 3.608 1254.088 53.590 -0.842 0.535 -1.931 0.759 1624.987 4.291 28.966 0.072 61 60 71 10 - 1.057 0.728 13.646 0.029 0.034 0.000 23.918 0.334 0.052 0.001 1631.675 116.506 1124.720 88.785 -3.940 2.101 -0.651 0.045 1688.805 101.923 57.782 14.540 62 109 113 10 - 1.060 0.681 12.545 0.000 0.000 0.000 19.286 0.000 0.059 0.000 1484.197 0.004 920.633 17.258 -2.448 0.516 -2.606 0.000 1529.520 0.000 47.929 0.002 63 80 91 10 - 1.140 0.825 5.592 0.000 0.069 0.000 17.456 0.000 0.109 0.000 1030.130 0.012 1601.830 27.680 5.160 0.616 0.752 0.000 1125.423 0.004 94.540 0.008 64 61 22 10 - 1.547 0.489 12.884 0.000 0.000 0.000 18.658 0.000 0.062 0.000 1287.670 0.000 1227.920 26.361 2.087 0.630 -1.563 0.000 1328.707 0.004 42.597 0.002 65 65 142 10 - 1.609 0.465 13.598 0.001 0.000 0.000 20.523 0.000 0.053 0.000 1812.180 0.007 1242.125 9.410 4.169 0.487 -8.600 0.001 1837.472 0.004 33.893 0.006 66 63 2 10 - 1.618 0.620 11.163 0.000 0.052 0.000 19.921 0.000 0.074 0.000 1612.010 0.007 1142.242 17.089 0.629 0.472 -4.038 0.000 1640.850 0.000 32.880 0.004 67 71 79 10 - 1.719 0.983 12.761 0.000 0.000 0.000 18.973 0.000 0.060 0.000 1428.622 0.004 1202.068 29.316 6.850 1.082 -7.824 0.000 1463.520 0.000 42.716 0.002 68 69 53 10 - 1.771 1.118 14.068 0.000 0.000 0.000 22.330 0.000 0.046 0.000 1316.773 0.004 1285.473 14.217 6.192 1.087 -4.974 0.001 1335.790 0.000 23.991 0.001 69 67 21 10 - 1.840 0.428 10.784 0.000 0.034 0.000 19.322 0.000 0.072 0.000 1285.688 0.008 1117.495 10.149 -0.691 0.439 0.523 0.001 1318.855 0.005 32.646 0.006 70 70 134 10 - 1.845 0.422 11.423 0.000 0.000 0.000 19.694 0.000 0.058 0.000 1223.665 0.005 1143.160 12.317 3.324 0.532 -2.622 0.000 1254.850 0.000 33.809 0.003 71 66 28 10 - 2.156 0.092 16.901 0.145 0.000 0.000 25.946 0.295 0.035 0.000 1664.168 128.023 953.917 39.846 -2.267 2.191 -3.344 0.114 1727.315 172.192 66.488 44.052 72 72 51 10 - 2.177 0.345 14.563 0.000 0.052 0.000 24.598 0.000 0.056 0.000 1316.715 0.009 1570.730 16.814 6.253 0.181 -2.070 0.000 1368.102 0.004 53.459 0.004 73 68 5 10 - 2.186 0.209 10.791 0.000 0.000 0.000 17.361 0.000 0.071 0.000 1320.465 0.009 1352.238 23.403 4.872 0.278 -2.775 0.000 1358.330 0.000 40.637 0.005 74 73 52 10 - 2.462 0.437 11.857 0.000 0.034 0.000 21.481 0.000 0.062 0.000 1332.390 0.007 1331.270 18.518 3.857 0.469 -2.157 0.000 1405.307 0.004 75.072 0.005 75 75 117 10 - 2.591 1.501 5.582 0.000 0.017 0.000 10.747 0.000 0.156 0.000 1471.223 0.004 1131.087 27.013 -0.164 1.301 -1.468 0.000 1551.900 0.000 82.145 0.003 76 76 121 10 - 2.757 0.190 15.413 0.030 0.000 0.000 23.407 0.072 0.042 0.000 1441.680 23.042 1181.880 26.999 2.544 0.494 -2.763 0.841 1476.762 16.185 37.844 6.016 77 74 8 10 - 2.804 0.346 9.774 0.000 0.000 0.000 15.587 0.000 0.084 0.000 1031.230 0.012 1151.565 3.228 4.639 0.312 -0.954 0.002 1062.565 0.005 32.287 0.005 78 77 125 10 - 2.956 0.265 9.059 0.000 0.000 0.000 14.582 0.000 0.093 0.000 1332.722 0.004 1325.645 17.543 -0.222 0.167 2.522 0.000 1393.822 0.004 58.576 0.004 79 79 148 10 - 3.338 0.337 9.501 0.000 0.017 0.000 16.813 0.000 0.082 0.000 1373.653 0.004 1326.715 10.338 2.499 0.388 0.027 0.000 1407.895 0.005 34.216 0.003 80 78 43 10 - 3.420 0.161 13.876 0.062 0.000 0.000 24.966 0.181 0.038 0.000 1203.815 13.490 1353.628 21.704 3.673 0.639 0.968 0.680 1232.450 11.316 27.667 1.490 81 85 90 10 - 3.499 0.582 11.694 0.000 0.000 0.000 19.420 0.000 0.059 0.000 1524.062 0.008 1254.383 26.891 2.957 0.549 -2.600 0.000 1566.020 0.000 44.559 0.004 82 96 144 10 - 3.736 1.983 14.597 0.155 0.000 0.000 23.244 0.913 0.043 0.003 1638.918 27.535 1089.932 148.738 -1.437 2.850 -0.736 0.937 1680.150 26.411 41.970 7.550 83 83 81 10 - 4.181 0.676 10.556 0.000 0.017 0.000 19.500 0.000 0.066 0.000 1679.600 0.000 1209.035 23.242 8.004 0.495 -8.994 0.001 1717.150 0.000 46.546 0.001 84 86 126 10 - 4.231 0.820 13.402 0.000 0.000 0.000 22.864 0.000 0.045 0.000 1437.102 0.004 1009.162 9.760 -0.405 0.755 -0.675 0.000 1539.537 0.004 103.107 0.001 85 82 35 10 - 4.429 0.243 13.516 0.086 0.000 0.000 21.373 0.051 0.050 0.001 1422.540 1.230 1373.582 45.688 4.605 0.121 -1.357 0.944 1490.320 18.770 69.143 18.482 86 108 84 10 - 4.431 2.539 5.560 0.856 0.060 0.015 12.118 0.730 0.154 0.019 2052.713 82.831 1181.928 181.411 2.306 1.076 -7.277 0.965 2114.883 74.846 69.446 7.018 87 81 10 10 - 4.533 0.147 13.434 0.000 0.000 0.000 20.796 0.000 0.052 0.000 1313.870 0.017 1106.747 9.549 4.643 0.101 -2.606 0.002 1353.747 0.004 42.483 0.009 88 84 118 10 - 4.597 0.401 14.224 0.000 0.000 0.000 21.784 0.000 0.048 0.000 812.933 0.006 1561.932 19.206 6.094 0.589 5.630 0.001 854.980 0.002 36.417 0.005 89 87 133 10 - 4.605 0.650 12.937 0.000 0.000 0.000 23.370 0.000 0.043 0.000 1314.115 0.005 955.893 27.114 0.978 0.632 -0.502 0.000 1368.153 0.004 54.539 0.003 90 106 18 10 - 4.806 0.311 13.463 0.000 0.000 0.000 24.373 0.001 0.040 0.000 1207.367 0.004 1226.390 11.365 7.546 0.398 -2.879 0.000 1237.415 0.005 32.926 0.001 91 88 9 10 - 4.811 1.015 17.516 0.000 0.000 0.000 26.890 0.000 0.033 0.000 1593.650 0.007 852.707 14.236 -3.510 1.086 0.360 0.000 1649.222 0.004 55.215 0.003 92 89 76 10 - 4.921 0.828 8.479 0.001 0.121 0.000 16.155 0.009 0.123 0.000 1675.845 1.210 1128.490 24.540 5.340 0.543 -6.340 0.197 1714.182 0.917 44.677 0.098 93 92 135 10 - 5.104 0.801 12.373 0.000 0.000 0.000 21.291 0.001 0.051 0.000 1682.297 0.008 879.111 26.874 0.911 0.548 -4.271 0.002 1721.285 0.005 43.257 0.003 94 91 101 10 - 5.127 0.529 14.134 0.000 0.069 0.000 22.851 0.000 0.067 0.000 1774.452 0.004 1143.035 25.663 5.251 0.622 -6.708 0.000 1794.785 0.005 27.042 0.002 95 93 68 10 - 5.267 0.116 13.506 0.000 0.000 0.000 23.168 0.000 0.044 0.000 1270.545 0.042 903.954 16.269 3.013 0.114 -3.875 0.000 1513.010 0.016 246.341 0.028 96 90 98 10 - 5.488 0.197 12.076 0.000 0.052 0.000 22.598 0.000 0.064 0.000 1417.480 0.000 1486.365 17.352 4.645 0.302 1.068 0.000 1464.918 0.004 46.366 0.002 97 95 78 10 - 5.560 0.457 16.706 0.008 0.000 0.000 25.451 0.140 0.036 0.000 1842.725 31.353 944.442 50.103 0.728 0.730 -4.713 0.093 1894.173 29.224 56.160 2.221 98 94 24 10 - 5.636 0.329 8.495 0.000 0.034 0.000 14.545 0.000 0.106 0.000 1438.640 0.007 1052.645 15.771 1.940 0.237 -0.598 0.000 1481.457 0.004 43.412 0.003 99 98 82 10 - 5.912 1.108 9.062 0.000 0.000 0.000 15.621 0.000 0.085 0.000 1579.757 0.022 1004.099 15.653 5.426 1.168 -6.184 0.000 1665.025 0.011 91.451 0.016 100 100 102 10 - 6.178 0.304 7.429 0.009 0.000 0.000 13.326 0.125 0.110 0.002 1579.557 20.718 876.049 15.882 3.925 2.192 -5.419 1.923 1637.915 20.785 63.778 1.855 101 101 73 10 - 6.491 1.286 5.274 1.121 0.112 0.009 9.331 1.965 0.220 0.043 1572.305 148.870 1132.720 36.265 8.968 1.519 -7.591 0.267 1636.495 138.775 71.783 10.363 102 97 95 10 - 6.500 0.357 14.891 0.012 0.000 0.000 22.738 0.016 0.044 0.000 1324.383 41.675 1347.323 23.736 7.302 0.979 -1.935 0.308 1458.680 26.090 136.237 15.891 103 103 16 10 - 6.598 0.717 13.543 0.000 0.000 0.000 25.565 0.000 0.037 0.000 1435.965 0.023 965.739 17.475 4.647 0.755 -3.499 0.000 1507.220 0.007 74.752 0.014 104 113 131 10 - 6.748 0.706 11.362 0.097 0.000 0.000 21.172 0.035 0.052 0.000 1272.642 14.128 1152.102 20.187 2.181 0.890 2.808 0.199 1330.730 20.670 55.278 6.741 105 99 26 10 - 6.777 0.221 14.549 0.000 0.034 0.000 22.246 0.000 0.057 0.000 1337.785 0.005 1237.665 9.368 12.623 0.281 -7.317 0.000 1377.372 0.004 46.903 0.001 106 111 140 10 - 6.779 0.467 13.408 0.000 0.000 0.000 21.842 0.000 0.048 0.000 1701.625 0.009 1130.092 12.459 7.382 0.510 -6.848 0.000 1747.780 0.000 53.005 0.004 107 102 70 10 - 6.859 0.368 14.104 0.000 0.034 0.000 23.831 0.000 0.053 0.000 1421.310 0.007 1245.168 28.046 7.072 0.205 -2.606 0.000 1481.862 0.004 63.157 0.003 108 104 128 10 - 6.979 0.272 7.750 0.000 0.000 0.000 15.894 0.000 0.086 0.000 1565.898 0.004 1165.102 17.917 2.422 0.296 0.114 0.000 1609.468 0.004 43.454 0.002 109 105 37 10 - 7.074 0.273 11.212 0.000 0.017 0.000 19.176 0.000 0.066 0.000 1435.567 0.004 1069.815 30.137 5.507 0.352 -2.716 0.000 1495.420 0.000 62.566 0.003 110 107 63 10 - 7.255 0.593 12.974 0.000 0.017 0.000 23.438 0.000 0.049 0.000 1090.135 0.005 1330.148 10.453 2.694 0.583 6.481 0.000 1144.622 0.004 48.006 0.003 111 110 141 10 - 7.577 0.087 14.993 0.000 0.000 0.000 26.718 0.000 0.034 0.000 1348.737 0.004 1125.025 15.059 3.369 0.154 1.314 0.001 1415.803 0.004 65.755 0.004 112 112 39 10 - 7.717 1.437 13.076 0.000 0.034 0.000 21.292 0.000 0.062 0.000 1418.793 0.004 1031.657 36.860 7.200 1.546 -3.905 0.000 1469.900 0.000 55.008 0.004 113 115 87 10 - 7.749 0.454 13.090 0.000 0.000 0.000 23.222 0.000 0.044 0.000 1476.158 0.011 1272.345 14.120 8.203 0.331 -3.187 0.001 1542.362 0.004 69.394 0.007 114 114 19 10 - 8.156 0.557 9.610 0.000 0.000 0.000 14.939 0.000 0.089 0.000 1217.220 0.000 1305.247 14.882 12.752 0.458 -4.164 0.000 1257.840 0.000 44.788 0.001 115 121 145 10 - 8.234 0.328 10.233 0.000 0.000 0.000 18.503 0.000 0.065 0.000 1947.057 0.004 867.776 31.685 3.537 0.526 -6.582 0.000 1988.970 0.000 48.495 0.001 116 119 136 10 - 8.348 0.416 14.705 0.000 0.034 0.000 25.924 0.000 0.047 0.000 1386.100 0.007 1184.423 17.051 4.270 0.435 1.673 0.001 1426.608 0.004 38.834 0.003 117 122 108 10 - 8.381 0.460 14.681 0.085 0.000 0.000 23.063 0.127 0.043 0.001 1232.655 19.625 1256.318 24.006 9.329 0.902 -1.541 0.488 1314.030 2.905 82.916 16.234 118 118 59 10 - 8.410 0.499 14.607 0.000 0.000 0.000 22.480 0.000 0.045 0.000 1369.202 0.004 1270.800 13.880 9.935 0.543 -3.034 0.000 1418.590 0.000 52.421 0.003 119 117 6 10 - 8.515 0.753 15.939 0.155 0.000 0.000 24.412 0.259 0.039 0.000 1449.795 8.149 1040.126 30.813 3.445 1.306 -0.055 0.320 1552.490 52.943 102.751 44.470 120 116 25 10 - 8.519 0.328 14.667 0.000 0.034 0.000 24.106 0.000 0.052 0.000 1754.810 0.000 914.418 13.386 7.544 0.397 -8.388 0.000 1842.332 0.004 95.912 0.001 121 123 67 10 - 8.816 0.536 10.832 0.000 0.000 0.000 18.596 0.000 0.064 0.000 1463.985 0.005 1034.602 12.469 6.496 0.480 -2.527 0.000 1516.725 0.005 55.269 0.003 122 120 109 10 - 8.886 0.324 13.897 0.000 0.000 0.000 22.887 0.000 0.044 0.000 1739.505 0.005 1021.742 10.450 10.462 0.263 -9.293 0.000 1784.128 0.004 53.917 0.000 123 126 116 10 - 9.037 0.868 13.219 0.286 0.000 0.000 25.431 1.049 0.038 0.003 1717.020 26.917 1053.345 24.494 5.122 1.014 -4.705 1.799 1910.625 57.426 198.310 32.310 124 127 110 10 - 9.102 0.544 12.595 0.000 0.000 0.000 20.109 0.000 0.055 0.000 1458.440 0.000 1326.795 8.218 10.158 0.491 -2.662 0.000 1484.760 0.000 28.977 0.001 125 128 94 10 - 9.273 0.182 11.377 0.000 0.000 0.000 20.295 0.000 0.055 0.000 1350.680 0.007 1263.432 15.692 4.961 0.186 3.037 0.000 1394.020 0.000 40.300 0.003 126 124 13 10 - 9.465 0.169 13.992 0.000 0.000 0.000 23.157 0.000 0.043 0.000 1146.433 0.013 1120.465 15.556 10.227 0.270 -1.592 0.000 1201.948 0.004 57.108 0.007 127 130 45 10 - 9.550 0.386 9.814 0.000 0.017 0.000 16.010 0.001 0.087 0.000 1554.797 0.004 1074.615 29.539 8.300 0.409 -4.112 0.000 1606.680 0.000 55.995 0.002 128 135 152 10 - 9.610 0.259 15.446 0.000 0.000 0.000 23.011 0.000 0.043 0.000 1665.850 0.000 946.076 8.652 5.728 0.268 -4.098 0.000 1739.930 0.000 78.180 0.001 129 125 93 10 - 9.689 0.119 13.345 0.366 0.000 0.000 23.264 0.111 0.043 0.000 1423.375 94.377 1040.887 98.513 5.578 0.171 -0.319 2.153 1483.550 109.385 60.492 17.162 130 133 115 10 - 9.787 0.539 13.502 0.000 0.034 0.000 22.814 0.000 0.056 0.000 1637.325 0.005 1220.587 16.638 9.947 0.458 -4.921 0.001 1691.818 0.004 59.413 0.004 131 131 114 10 - 9.826 0.114 13.465 0.000 0.000 0.000 20.399 0.000 0.053 0.000 1818.070 0.000 1053.033 18.751 9.771 0.258 -8.246 0.000 1874.900 0.000 65.072 0.001 132 129 3 10 - 10.018 0.127 14.428 0.000 0.034 0.000 22.032 0.000 0.058 0.000 1549.895 0.005 1118.065 42.148 12.787 0.454 -7.537 0.001 1587.460 0.000 45.103 0.003 133 132 119 10 - 10.143 0.318 14.591 0.000 0.000 0.000 23.723 0.000 0.041 0.000 2030.400 0.000 983.656 8.263 4.708 0.325 -5.477 0.000 2069.310 0.000 44.387 0.001 134 136 150 10 - 10.431 0.253 14.509 0.338 0.073 0.007 23.445 0.046 0.067 0.003 2007.825 335.507 1296.773 80.914 10.058 1.357 -7.287 5.448 2055.438 339.336 54.902 9.277 135 150 137 10 - 10.486 0.981 13.674 0.276 0.026 0.009 21.535 0.203 0.057 0.004 1802.435 67.949 850.777 19.785 5.939 1.057 -6.012 0.908 1900.545 36.937 104.120 32.144 136 134 96 10 - 10.666 0.361 14.905 0.000 0.000 0.000 23.611 0.000 0.042 0.000 1180.222 0.008 1197.192 20.594 9.497 0.535 0.430 0.001 1271.465 0.005 90.810 0.004 137 145 130 10 - 10.686 0.215 10.825 0.001 0.069 0.000 18.924 0.000 0.085 0.000 1267.947 0.004 1066.520 11.839 6.859 0.271 0.757 0.000 1374.340 0.000 105.638 0.005 138 137 97 10 - 10.744 0.356 11.161 0.121 0.000 0.000 17.162 0.102 0.071 0.000 1500.715 119.809 1067.945 5.794 12.386 1.759 -6.461 0.315 1543.383 131.415 49.125 11.293 139 138 89 10 - 10.796 0.255 8.739 0.000 0.017 0.000 14.675 0.000 0.099 0.000 1540.630 0.000 1060.565 11.528 12.264 0.289 -6.895 0.000 1596.385 0.005 62.650 0.001 140 141 122 10 - 10.930 0.437 14.198 0.141 0.000 0.000 23.447 0.395 0.043 0.001 1390.735 77.045 1002.527 29.545 8.394 0.193 -1.835 0.884 1437.828 84.728 48.932 8.567 141 139 50 10 - 10.969 0.619 10.602 0.000 0.000 0.000 18.906 0.000 0.063 0.000 1799.200 0.000 766.240 37.212 1.470 0.550 -1.686 0.000 1882.990 0.000 85.470 0.001 142 147 120 10 - 11.521 0.159 4.285 0.000 0.121 0.000 8.527 0.000 0.243 0.000 1526.737 0.004 1528.830 15.598 15.387 0.301 -5.049 0.000 1642.110 0.000 120.418 0.003 143 140 58 10 - 11.638 0.280 11.900 0.000 0.017 0.000 18.863 0.000 0.067 0.000 1899.500 0.000 1081.518 33.994 5.711 0.435 -2.672 0.000 1938.750 0.000 41.925 0.000 144 142 31 10 - 12.238 0.461 13.303 0.000 0.000 0.000 21.021 0.000 0.051 0.000 1406.755 0.009 1096.230 19.810 11.836 0.584 -3.236 0.000 1456.838 0.004 53.317 0.006 145 143 151 10 - 12.714 0.279 7.749 0.000 0.000 0.000 13.417 0.000 0.108 0.000 1964.388 0.004 896.694 19.473 6.427 0.348 -4.948 0.001 2015.227 0.004 55.788 0.002 146 144 129 10 - 12.743 0.384 13.927 0.169 0.000 0.000 20.877 0.157 0.051 0.001 1557.322 37.718 937.363 18.414 7.410 1.237 -1.420 1.619 1611.295 33.980 55.392 2.120 147 146 132 10 - 12.926 0.195 13.916 0.000 0.000 0.000 22.376 0.000 0.046 0.000 1836.933 0.004 878.615 11.559 11.218 0.259 -8.685 0.000 1909.210 0.000 80.959 0.002 148 148 99 10 - 13.625 0.374 9.809 0.371 0.000 0.000 21.326 1.560 0.054 0.006 1819.340 7.577 948.136 21.599 10.081 0.705 -5.718 0.542 1868.615 8.389 54.990 1.051 149 149 86 10 - 14.127 0.142 12.241 0.000 0.000 0.000 20.385 0.001 0.054 0.000 1876.680 0.000 793.395 14.295 7.999 0.164 -5.168 0.000 1917.780 0.000 46.262 0.001 150 151 139 10 - 14.803 0.643 14.398 0.000 0.000 0.000 22.842 0.000 0.044 0.000 1558.020 0.007 877.430 6.677 7.620 0.660 -0.349 0.000 1630.265 0.005 72.595 0.004 151 152 92 10 - 16.300 0.353 12.552 0.000 0.000 0.000 18.676 0.000 0.062 0.000 1163.448 0.008 1243.952 7.434 15.781 0.397 1.090 0.000 1187.940 0.000 23.400 0.002 152
How many clusters are generated?
Is this the same number that after refinement (see above)?
If not what could be the reason?
Answer expand_more
After rigid body docking the first acceptable cluster is at rank 41. After refinement it scores at the top with score significantly better than the second-ranked cluster!
We are providing in the scripts directory a simple script that extract some cluster statistics for acceptable or better clusters from the caprieval steps.
To use is simply call the script with as argument the run directory you want to analyze, e.g.:
./scripts/extract-capri-stats-clt.sh ./runs/scenario1-surface
View the output of the script expand_more
============================================== == ./runs/scenario1-surface//4_caprieval/capri_clt.tsv ============================================== Total number of acceptable or better clusters: 2 out of 152 Total number of medium or better clusters: 1 out of 152 Total number of high quality clusters: 0 out of 152 First acceptable cluster - rank: 43 i-RMSD: 2.535 Fnat: 0.345 DockQ: 0.423 First medium cluster - rank: 54 i-RMSD: 1.684 Fnat: 0.526 DockQ: 0.622 Best cluster - rank: 54 i-RMSD: 1.684 Fnat: 0.526 DockQ: 0.622 ============================================== == ./runs/scenario1-surface//9_caprieval/capri_clt.tsv ============================================== Total number of acceptable or better clusters: 2 out of 127 Total number of medium or better clusters: 1 out of 127 Total number of high quality clusters: 0 out of 127 First acceptable cluster - rank: 1 i-RMSD: 1.678 Fnat: 0.733 DockQ: 0.669 First medium cluster - rank: 1 i-RMSD: 1.678 Fnat: 0.733 DockQ: 0.669 Best cluster - rank: 1 i-RMSD: 1.678 Fnat: 0.733 DockQ: 0.669
Similarly some simple statistics can be extracted from the single model caprieval capri_ss.tsv files with the extract-capri-stats.sh script:
./scripts/extract-capri-stats.sh ./runs/scenario1-surface
View the output of the script: expand_more
============================================== == ./runs/scenario1-surface/4_caprieval/capri_ss.tsv ============================================== Total number of acceptable or better models: 20 out of 1520 Total number of medium or better models: 8 out of 1520 Total number of high quality models: 0 out of 1520 First acceptable model - rank: 344 i-RMSD: 2.535 Fnat: 0.345 DockQ: 0.423 First medium model - rank: 491 i-RMSD: 1.282 Fnat: 0.707 DockQ: 0.738 Best model - rank: 559 i-RMSD: 1.282 Fnat: 0.707 DockQ: 0.738 ============================================== == ./runs/scenario1-surface/9_caprieval/capri_ss.tsv ============================================== Total number of acceptable or better models: 22 out of 1475 Total number of medium or better models: 13 out of 1475 Total number of high quality models: 0 out of 1475 First acceptable model - rank: 1 i-RMSD: 1.518 Fnat: 0.810 DockQ: 0.722 First medium model - rank: 1 i-RMSD: 1.518 Fnat: 0.810 DockQ: 0.722 Best model - rank: 17 i-RMSD: 1.197 Fnat: 0.879 DockQ: 0.811
Note that this kind of analysis only makes sense when we know the reference complex and for benchmarking / performance analysis purposes.
Look at the single structure statistics provided by the script
Answer expand_more
In terms of iRMSD values we only observe very small differences in the best models, but the change in ranking is impressive! The fraction of native contacts and the DockQ scores are however improving much more after flexible refinement. All this will of course depend on how different are the bound and unbound conformations and the amount of data used to drive the docking process. In general, from our experience, the more and better data at hand, the larger the conformational changes that can be induced.
Is the best model always ranked as first?
Answer expand_more
This is clearly not the case. The scoring function is not perfect, but does a reasonable job in ranking models of acceptable or better quality on top in this case.
Analysis scenario 1: visualising the scores and their components
We have precalculated a number of interactive plots to visualize the scores and their components versus ranks and model quality.
Models statistics:
- iRMSD versus HADDOCK score
- DockQ versus HADDOCK score
- DockQ versus van der Waals energy
- DockQ versus electrostatic energy
- DockQ versus ambiguous restraints energy
- DockQ versus desolvation energy
Cluster statistics (distributions of values per cluster ordered according to their HADDOCK rank):
- HADDOCK scores
- van der Waals energies
- electrostatic energies
- ambiguous restraints energies
- desolvation energies
Analysis scenario 2a: Paratope - NMR-epitope as passive
Let us now analyse the docking results for this scenario. Use for that either your own run or a pre-calculated run provided in the runs directory.
Go into the analysis/9_caprieval_analysis directory of the respective run directory and
Inspect the final cluster statistics in capri_clt.tsv file
View the pre-calculated 9_caprieval/capri_clt.tsv file expand_more
cluster_rank cluster_id n under_eval score score_std irmsd irmsd_std fnat fnat_std lrmsd lrmsd_std dockq dockq_std air air_std bsa bsa_std desolv desolv_std elec elec_std total total_std vdw vdw_std caprieval_rank 1 7 10 - -138.617 3.623 1.302 0.095 0.759 0.042 3.654 0.845 0.723 0.042 106.923 15.255 2007.338 29.881 4.998 2.064 -535.045 31.312 -475.421 23.968 -47.299 4.337 1 2 2 17 - -114.732 8.026 14.934 0.048 0.069 0.000 23.085 0.282 0.066 0.001 160.053 15.937 1925.930 68.200 4.355 4.005 -383.893 65.058 -282.153 44.813 -58.313 7.769 2 3 6 10 - -94.885 3.118 5.158 0.190 0.142 0.014 12.677 0.697 0.177 0.010 195.712 3.139 1678.185 4.775 8.844 0.929 -326.919 4.813 -189.123 5.020 -57.916 4.522 3 4 1 20 - -85.733 5.280 8.889 0.683 0.116 0.049 17.160 0.949 0.115 0.023 212.853 21.459 1542.527 57.393 6.435 2.591 -328.754 32.768 -163.602 15.475 -47.702 7.750 4 5 5 10 - -77.835 3.974 4.405 0.344 0.207 0.086 10.394 1.197 0.239 0.050 177.651 29.362 1644.388 54.484 11.269 2.084 -365.089 43.590 -221.289 30.831 -33.852 8.784 5 6 4 10 - -69.846 2.776 6.854 0.076 0.142 0.007 14.212 0.179 0.150 0.004 305.336 14.743 1491.412 41.939 4.152 1.676 -302.880 31.549 -41.500 23.024 -43.955 4.249 6 7 3 10 - -52.284 6.453 4.930 0.161 0.125 0.033 12.482 0.704 0.176 0.018 356.568 28.814 1228.580 69.244 5.359 1.823 -299.986 38.202 23.279 48.112 -33.303 2.374 7
How many clusters are generated?
Since for this tutorial we have at hand the crystal structure of the complex, we provided it as reference to the caprieval modules.
This means that the iRMSD, lRMSD, Fnat and DockQ statistics report on the quality of the docked model compared to the reference crystal structure.
How many clusters of acceptable or better quality have been generate according to CAPRI criteria?
What is the rank of the best cluster generated?
What is the rank of the first acceptable of better cluster generated?
In this run we also had a caprieval after the clustering of the rigid body models (step 4 of our workflow).
Inspect the corresponding capri_clt.tsv file
View the pre-calculated 4_caprieval/capri_clt.tsv file expand_more
cluster_rank cluster_id n under_eval score score_std irmsd irmsd_std fnat fnat_std lrmsd lrmsd_std dockq dockq_std air air_std bsa bsa_std desolv desolv_std elec elec_std total total_std vdw vdw_std caprieval_rank 1 1 10 - -7.065 0.204 14.798 0.000 0.069 0.000 23.304 0.000 0.066 0.000 800.213 0.006 1705.220 15.183 3.034 0.336 -1.039 0.001 798.194 0.002 -0.980 0.003 1 2 4 10 - -4.905 0.322 1.247 0.000 0.690 0.000 2.258 0.000 0.738 0.000 830.946 0.006 1750.490 10.557 12.935 0.295 -8.707 0.001 828.476 0.002 6.237 0.004 2 3 5 10 - -3.218 0.321 12.988 0.000 0.069 0.000 21.389 0.000 0.073 0.000 1250.720 0.007 1281.875 12.910 -2.070 0.282 -1.521 0.000 1317.727 0.004 68.529 0.003 3 4 6 10 - -2.754 0.136 5.104 0.000 0.138 0.000 12.428 0.000 0.179 0.000 1109.805 0.005 1381.213 18.673 3.933 0.265 -4.214 0.000 1129.680 0.000 24.088 0.003 4 5 3 10 - -2.534 0.181 8.639 0.000 0.121 0.000 16.823 0.000 0.118 0.000 1115.398 0.004 1139.723 20.158 4.226 0.286 -6.851 0.000 1141.970 0.000 33.428 0.001 5 6 2 10 - 0.099 0.314 9.991 0.000 0.052 0.000 18.505 0.001 0.083 0.000 1069.392 0.061 1148.727 27.538 7.879 0.518 -7.227 0.001 1086.138 0.023 23.972 0.039 6 7 8 10 - 3.994 0.158 4.033 0.001 0.121 0.000 10.360 0.000 0.215 0.000 1343.840 0.000 1164.535 21.845 7.108 0.196 -5.423 0.000 1390.040 0.000 51.623 0.001 7 8 9 10 - 4.619 0.267 7.100 0.000 0.121 0.000 14.167 0.000 0.143 0.000 1523.870 0.007 1134.912 25.058 6.563 0.123 -6.186 0.000 1552.900 0.000 35.217 0.004 8 9 7 10 - 10.174 0.445 4.776 0.000 0.086 0.000 11.416 0.000 0.178 0.000 1954.290 0.000 937.232 7.379 10.179 0.376 -10.952 0.000 2021.017 0.004 77.678 0.002 9
How many clusters are generated?
Is this the same number that after refinement (see above)?
If not what could be the reason?
Answer expand_more
After rigid body docking the first acceptable cluster is at rank 2. After refinement it scores at the top with score significantly better than the second-ranked cluster.
Did the rank improve after refinement?
We are providing in the scripts a simple script that extract some cluster statistics for acceptable or better clusters from the caprieval steps.
To use is simply call the script with as argument the run directory you want to analyze, e.g.:
./scripts/extract-capri-stats-clt.sh ./runs/scenario2a-NMR-epitope-pass
View the output of the script expand_more
============================================== == ./runs/scenario2a-NMR-epitope-pass/4_caprieval/capri_clt.tsv ============================================== Total number of acceptable or better clusters: 1 out of 9 Total number of medium or better clusters: 1 out of 9 Total number of high quality clusters: 0 out of 9 First acceptable cluster - rank: 2 i-RMSD: 1.247 Fnat: 0.690 DockQ: 0.738 First medium cluster - rank: 2 i-RMSD: 1.247 Fnat: 0.690 DockQ: 0.738 Best cluster - rank: 2 i-RMSD: 1.247 Fnat: 0.690 DockQ: 0.738 ============================================== == ./runs/scenario2a-NMR-epitope-pass/9_caprieval/capri_clt.tsv ============================================== Total number of acceptable or better clusters: 1 out of 7 Total number of medium or better clusters: 1 out of 7 Total number of high quality clusters: 0 out of 7 First acceptable cluster - rank: 1 i-RMSD: 1.302 Fnat: 0.759 DockQ: 0.723 First medium cluster - rank: 1 i-RMSD: 1.302 Fnat: 0.759 DockQ: 0.723 Best cluster - rank: 1 i-RMSD: 1.302 Fnat: 0.759 DockQ: 0.723
Similarly some simple statistics can be extracted from the single model caprieval capri_ss.tsv files with the extract-capri-stats.sh script:
./scripts/extract-capri-stats.sh ./runs/scenario2a-NMR-epitope-pass
View the output of the script expand_more
============================================== == ./runs/scenario2a-NMR-epitope-pass/4_caprieval/capri_ss.tsv ============================================== Total number of acceptable or better models: 10 out of 90 Total number of medium or better models: 10 out of 90 Total number of high quality models: 1 out of 90 First acceptable model - rank: 11 i-RMSD: 1.247 Fnat: 0.690 DockQ: 0.738 First medium model - rank: 11 i-RMSD: 1.247 Fnat: 0.690 DockQ: 0.738 Best model - rank: 16 i-RMSD: 0.980 Fnat: 0.586 DockQ: 0.726 ============================================== == ./runs/scenario2a-NMR-epitope-pass/9_caprieval/capri_ss.tsv ============================================== Total number of acceptable or better models: 12 out of 87 Total number of medium or better models: 10 out of 87 Total number of high quality models: 0 out of 87 First acceptable model - rank: 1 i-RMSD: 1.300 Fnat: 0.793 DockQ: 0.730 First medium model - rank: 1 i-RMSD: 1.300 Fnat: 0.793 DockQ: 0.730 Best model - rank: 5 i-RMSD: 1.029 Fnat: 0.810 DockQ: 0.811
Note that this kind of analysis only makes sense when we know the reference complex and for benchmarking / performance analysis purposes.
Look at the single structure statistics provided by the script
Answer expand_more
In terms of iRMSD values we only observe very small differences with a slight increase. The fraction of native contacts and the DockQ scores are however improving much more after flexible refinement. All this will of course depend on how different are the bound and unbound conformations and the amount of data used to drive the docking process. In general, from our experience, the more and better data at hand, the larger the conformational changes that can be induced.
Is the best model always ranked as first?
Answer expand_more
This is clearly not the case. The scoring function is not perfect, but does a reasonable job in ranking models of acceptable or better quality on top in this case.
Analysis scenario 2a: visualizing the scores and their components
Using the default settings (option postprocess=true) in the config files, interactive plots have been automatically generated in the analysis directory of the run.
These are useful to visualise the scores and their components versus ranks and model quality.
Models statistics:
- iRMSD versus HADDOCK score
- DockQ versus HADDOCK score
- DockQ versus van der Waals energy
- DockQ versus electrostatic energy
- DockQ versus ambiguous restraints energy
- DockQ versus desolvation energy
Cluster statistics (distributions of values per cluster ordered according to their HADDOCK rank):
- HADDOCK scores
- van der Waals energies
- electrostatic energies
- ambiguous restraints energies
- desolvation energies
Analysis scenario 2b: Paratope - NMR-epitope as active
Let us now analyse the docking results for this scenario. Use for that either your own run or a pre-calculated run provided in the runs directory.
Go into the analysis/9_caprieval_analysis directory of the respective run directory and
Inspect the final cluster statistics in capri_clt.tsv file
View the pre-calculated 9_caprieval/capri_clt.tsv file expand_more
cluster_rank cluster_id n under_eval score score_std irmsd irmsd_std fnat fnat_std lrmsd lrmsd_std dockq dockq_std air air_std bsa bsa_std desolv desolv_std elec elec_std total total_std vdw vdw_std caprieval_rank 1 1 17 - -151.013 2.855 1.957 0.466 0.642 0.060 4.965 0.721 0.593 0.080 61.922 16.739 1986.370 29.972 6.632 4.202 -596.659 47.783 -579.241 41.814 -44.505 9.407 1 2 5 10 - -144.671 4.375 15.023 0.056 0.073 0.007 24.092 0.434 0.065 0.003 82.575 31.344 2050.332 52.230 1.109 1.544 -454.861 68.487 -435.350 64.144 -63.065 9.264 2 3 4 10 - -103.148 2.915 9.859 0.357 0.065 0.025 19.699 0.784 0.082 0.011 118.571 18.485 1422.492 48.831 1.077 3.734 -395.524 36.286 -313.930 36.565 -36.977 2.057 3 4 2 11 - -101.775 9.988 14.811 0.042 0.082 0.014 23.773 0.258 0.069 0.005 112.762 35.542 1733.245 136.770 5.903 1.639 -369.718 13.140 -301.966 31.881 -45.010 9.758 4 5 12 4 - -101.717 16.264 2.883 0.465 0.414 0.073 6.588 0.667 0.421 0.039 123.812 49.768 1620.057 171.832 8.321 3.108 -510.810 25.365 -407.254 30.156 -20.257 18.482 5 6 6 10 - -100.286 5.972 5.029 0.078 0.121 0.012 12.377 0.431 0.175 0.007 81.077 18.925 1527.888 25.942 6.652 1.287 -297.121 20.305 -271.666 30.603 -55.622 4.563 6 7 3 10 - -98.426 7.151 4.147 0.602 0.341 0.092 8.377 1.144 0.324 0.059 163.456 41.462 1654.400 57.204 -1.567 4.125 -331.139 27.013 -214.660 64.132 -46.976 4.973 7 8 9 8 - -91.198 8.435 3.061 0.163 0.509 0.029 7.763 0.751 0.417 0.024 95.083 5.502 1636.765 120.832 7.456 2.015 -383.475 21.166 -319.859 23.245 -31.468 7.111 8 9 10 8 - -89.350 5.243 14.907 0.197 0.095 0.019 24.223 0.525 0.072 0.006 108.123 28.325 1698.345 93.675 4.693 2.411 -294.506 48.615 -232.337 53.247 -45.954 8.366 9 10 7 10 - -78.992 5.846 7.589 0.167 0.164 0.008 16.501 0.352 0.137 0.002 141.345 58.004 1386.070 33.470 -0.716 1.791 -253.702 31.000 -154.028 33.843 -41.671 4.896 10 11 11 6 - -77.052 4.065 3.956 0.826 0.341 0.071 8.653 1.743 0.327 0.075 171.334 27.914 1501.757 87.948 6.200 3.838 -329.716 23.812 -192.825 44.069 -34.442 5.191 11 12 8 8 - -67.688 6.454 14.580 0.019 0.086 0.012 23.018 0.239 0.072 0.005 148.451 30.560 1652.513 97.272 3.496 1.602 -203.546 55.957 -100.415 43.751 -45.320 6.620 12
How many clusters of acceptable or better quality have been generate according to CAPRI criteria?
What is the rank of the best cluster generated?
What is the rank of the first acceptable of better cluster generated?
In this run we also had a caprieval after the clustering of the rigid body models (step 4 of our workflow).
Inspect the corresponding capri_clt.tsv file
View the pre-calculated 4_caprieval/capri_clt.tsv file expand_more
cluster_rank cluster_id n under_eval score score_std irmsd irmsd_std fnat fnat_std lrmsd lrmsd_std dockq dockq_std air air_std bsa bsa_std desolv desolv_std elec elec_std total total_std vdw vdw_std caprieval_rank 1 6 10 - -14.099 0.485 2.534 0.060 0.328 0.000 6.091 0.186 0.416 0.006 497.929 84.662 1549.405 36.228 12.766 0.474 -16.378 0.493 484.394 89.658 2.844 5.623 1 2 5 10 - -13.662 1.131 7.797 0.008 0.138 0.000 16.855 0.109 0.126 0.001 728.546 171.645 1173.928 15.754 -3.900 0.575 -5.855 0.132 777.477 174.737 54.786 8.386 2 3 1 10 - -11.313 0.323 1.048 0.090 0.737 0.026 2.716 0.487 0.772 0.017 393.784 59.151 1658.795 79.415 11.225 0.683 -9.950 0.631 390.030 72.124 6.196 17.950 3 4 3 10 - -9.839 0.266 5.023 0.016 0.168 0.007 12.101 0.046 0.194 0.003 408.853 105.262 1349.137 18.104 5.414 0.889 -5.624 0.400 380.563 108.924 -22.667 6.196 4 5 4 10 - -9.326 1.678 14.812 0.010 0.069 0.000 23.503 0.056 0.065 0.000 380.995 98.521 1677.188 22.301 5.271 1.050 -1.377 0.204 353.849 106.067 -25.768 7.771 5 7 11 10 - -9.256 0.749 4.689 0.384 0.237 0.019 10.175 0.794 0.248 0.021 997.843 119.928 1262.298 9.238 -4.968 0.214 -1.769 1.706 1008.617 125.287 12.542 8.265 6 6 2 10 - -8.233 0.486 10.223 0.245 0.026 0.015 21.128 0.934 0.062 0.009 581.415 155.264 1036.009 53.300 1.424 0.492 -5.174 1.459 582.590 159.417 6.348 8.379 7 8 7 10 - -3.262 0.604 14.741 0.012 0.069 0.000 23.565 0.052 0.065 0.000 676.043 49.459 1149.500 14.839 9.827 0.292 -8.472 0.095 679.402 52.646 11.831 3.553 8 10 8 10 - -2.096 1.711 3.685 0.709 0.272 0.041 8.101 1.996 0.321 0.068 708.926 377.133 1167.398 7.469 11.135 1.233 -8.820 2.498 717.466 390.544 17.360 15.407 9 9 9 10 - -1.996 0.489 3.210 0.084 0.332 0.026 8.203 0.501 0.343 0.009 398.137 131.501 1060.155 56.080 12.793 0.944 -8.149 1.179 387.985 134.607 -2.003 5.126 10 12 10 10 - -1.280 2.048 14.353 0.513 0.038 0.008 22.816 0.551 0.057 0.003 869.164 86.949 1255.027 53.327 6.427 3.491 -4.390 2.183 918.969 91.260 54.194 7.974 11 11 12 10 - -1.104 3.228 14.742 0.077 0.052 0.000 24.131 0.342 0.058 0.001 574.145 40.525 1146.227 48.875 4.858 2.295 -0.342 0.112 583.846 49.827 10.042 11.138 12
How many clusters are generated?
Is this the same number that after refinement (see above)?
If not what could be the reason?
Answer expand_more
After rigid body docking the first acceptable cluster is at rank 1 and the same is true after refinement, but the iRMSD values have improved.
Use the extract-capri-stats-clt.sh script to extract some simple cluster statistics for this run.
./scripts/extract-capri-stats-clt.sh runs/scenario2b-NMR-epitope-act/
View the output of the script expand_more
============================================== == runs/scenario2b-NMR-epitope-act//4_caprieval/capri_clt.tsv ============================================== Total number of acceptable or better clusters: 4 out of 12 Total number of medium or better clusters: 1 out of 12 Total number of high quality clusters: 0 out of 12 First acceptable cluster - rank: 1 i-RMSD: 2.534 Fnat: 0.328 DockQ: 0.416 First medium cluster - rank: 3 i-RMSD: 1.048 Fnat: 0.737 DockQ: 0.772 Best cluster - rank: 3 i-RMSD: 1.048 Fnat: 0.737 DockQ: 0.772 ============================================== == runs/scenario2b-NMR-epitope-act//9_caprieval/capri_clt.tsv ============================================== Total number of acceptable or better clusters: 4 out of 12 Total number of medium or better clusters: 1 out of 12 Total number of high quality clusters: 0 out of 12 First acceptable cluster - rank: 1 i-RMSD: 1.957 Fnat: 0.642 DockQ: 0.593 First medium cluster - rank: 1 i-RMSD: 1.957 Fnat: 0.642 DockQ: 0.593 Best cluster - rank: 1 i-RMSD: 1.957 Fnat: 0.642 DockQ: 0.593
Similarly some simple statistics can be extracted from the single model caprieval capri_ss.tsv files with the extract-capri-stats.sh script:
./scripts/extract-capri-stats.sh ./runs/scenario2b-NMR-epitope-pass
View the output of the script expand_more
============================================== == runs/scenario2b-NMR-epitope-act//4_caprieval/capri_ss.tsv ============================================== Total number of acceptable or better models: 34 out of 120 Total number of medium or better models: 10 out of 120 Total number of high quality models: 2 out of 120 First acceptable model - rank: 2 i-RMSD: 2.533 Fnat: 0.328 DockQ: 0.416 First medium model - rank: 11 i-RMSD: 1.035 Fnat: 0.724 DockQ: 0.757 Best model - rank: 19 i-RMSD: 0.978 Fnat: 0.741 DockQ: 0.779 ============================================== == runs/scenario2b-NMR-epitope-act//9_caprieval/capri_ss.tsv ============================================== Total number of acceptable or better models: 35 out of 112 Total number of medium or better models: 11 out of 112 Total number of high quality models: 4 out of 112 First acceptable model - rank: 1 i-RMSD: 2.431 Fnat: 0.586 DockQ: 0.515 First medium model - rank: 3 i-RMSD: 1.922 Fnat: 0.638 DockQ: 0.597 Best model - rank: 10 i-RMSD: 0.758 Fnat: 0.845 DockQ: 0.871
Note that this kind of analysis only makes sense when we know the reference complex and for benchmarking / performance analysis purposes.
Look at the single structure statistics provided by the script
Answer expand_more
In this case we observe a small improvement in terms of iRMSD values and quite some large improvement in the fraction of native contacts and the DockQ scores. Also the single model rankings have improved, but the top ranked model is not the best one.
Is the best model always ranked as first?
Answer expand_more
This is clearly not the case. The scoring function is not perfect, but does a reasonable job in ranking models of acceptable or better quality on top in this case.
Analysis scenario 2b: visualizing the scores and their components
We have precalculated a number of interactive plots to visualize the scores and their components versus ranks and model quality.
Models statistics:
- iRMSD versus HADDOCK score
- DockQ versus HADDOCK score
- DockQ versus van der Waals energy
- DockQ versus electrostatic energy
- DockQ versus ambiguous restraints energy
- DockQ versus desolvation energy
Cluster statistics (distributions of values per cluster ordered according to their HADDOCK rank):
- HADDOCK scores
- van der Waals energies
- electrostatic energies
- ambiguous restraints energies
- desolvation energies
Comparing the performance of the three scenarios
Clearly all three scenarios give good results with an acceptable cluster in all three cases ranked at the top:
==============================================
== ./runs/scenario1-surface/9_caprieval/capri_ss.tsv
==============================================
Total number of acceptable or better models: 22 out of 1475
Total number of medium or better models: 13 out of 1475
Total number of high quality models: 0 out of 1475
First acceptable model - rank: 1 i-RMSD: 1.518 Fnat: 0.810 DockQ: 0.722
First medium model - rank: 1 i-RMSD: 1.518 Fnat: 0.810 DockQ: 0.722
Best model - rank: 17 i-RMSD: 1.197 Fnat: 0.879 DockQ: 0.811
==============================================
== runs/scenario2b-NMR-epitope-act//4_caprieval/capri_clt.tsv
==============================================
Total number of acceptable or better clusters: 4 out of 12
Total number of medium or better clusters: 1 out of 12
Total number of high quality clusters: 0 out of 12
First acceptable cluster - rank: 1 i-RMSD: 2.534 Fnat: 0.328 DockQ: 0.416
First medium cluster - rank: 3 i-RMSD: 1.048 Fnat: 0.737 DockQ: 0.772
Best cluster - rank: 3 i-RMSD: 1.048 Fnat: 0.737 DockQ: 0.772
==============================================
== runs/scenario2b-NMR-epitope-act//9_caprieval/capri_clt.tsv
==============================================
Total number of acceptable or better clusters: 4 out of 12
Total number of medium or better clusters: 1 out of 12
Total number of high quality clusters: 0 out of 12
First acceptable cluster - rank: 1 i-RMSD: 1.957 Fnat: 0.642 DockQ: 0.593
First medium cluster - rank: 1 i-RMSD: 1.957 Fnat: 0.642 DockQ: 0.593
Best cluster - rank: 1 i-RMSD: 1.957 Fnat: 0.642 DockQ: 0.593The best models are obtained when combining the information about the paratope with the NMR epitope defined as passive for HADDOCK, which is also the scenario described in our Structure 2020 article:
- F. Ambrosetti, B. Jiménez-García, J. Roel-Touris and A.M.J.J. Bonvin. Modeling Antibody-Antigen Complexes by Information-Driven Docking. Structure, 28, 119-129 (2020). Preprint freely available from here.
What is striking here is that the surface-based protocol (scenario1) is givin now thanks to the clustering step after the rigid-body docking step an excellent solution ranking on top, while these would not make through the refinement stage in the static HADDOCK2.4 protocol (or only very few that would not cluster at the end). Check for comparison our the related HADDOCK2.4 tutorial where you can find l-RMSD values for the surface scenario. Of course, due to the increased sampling it is also more costly.
Visualization of the models
To visualize the models from top cluster of your favorite run, start PyMOL and load the cluster representatives you want to view, e.g. this could be the top model from cluster1 of scenario2a.
These can be found in the runs/scenario2a-NMR-epitope-pass/8_seletopclusts/ directory
File menu -> Open -> select cluster_1_model_1.pdb
If you want to get an impression of how well defined a cluster is, repeat this for the best N models you want to view (cluster_1_model_X.pdb).
Also load the reference structure from the pdbs directory, 4G6M-matched.pdb.
PyMol can also be started from the command line with as argument all the PDB files you want to visualize, e.g.:
pymol runs/scenario2a-NMR-epitope-pass/8seletopclusts/cluster_1_model[1-4].pdb pdbs/4G6M-matched.pdb
Once all files have been loaded, type in the PyMOL command window:
show cartoon util.cbc color yellow, 4G6M_matched
Let us then superimpose all models on the reference structure:
Let’s now check if the active residues which we have defined (the paratope and epitope) are actually part of the interface. In the PyMOL command window type:
select paratope, (resi 31+32+33+34+35+52+54+55+56+100+101+102+103+104+105+106+1031+1032+1049+1050+1053+1091+1092+1093+1094+1096 and chain A) color red, paratope select epitope, (resi 72+73+74+75+81+83+84+89+90+92+94+96+97+98+115+116+117 and chain B) color orange, epitope
Are the residues of the paratope and NMR epitope at the interface?
Note: You can turn on and off a model by clicking on its name in the right panel of the PyMOL window.
See the overlay of the best model onto the reference structure expand_more
Top4 models of the top cluster of scenario2a superimposed onto the reference crystal structure (in yellow)
Conclusions
We have demonstrated three different scenarios for antibody-antigen modelling, all making use of the paratope information on the antibody side and either no information (surface) or a NMR-mapped epitope for the other two scenarios. Compared to the static HADDOCK2.X workflow, the modularity and flexibility of HADDOCK3 allowed to implement a clustering step after rigid-body sampling and select all resulting clusters for refinement. This strategy led to excellent results in this case while no single acceptable cluster was obtained with HADDOCK2.4. While HADDOCK3 is still very much work in progress, those results indicate already that we should be able to improve the performance of antibody-antigen modelling compared to the results we presented in our Structure 2020 article and in the related HADDOCK2.4 tutorial.
Congratulations! 🎉
You have completed this tutorial. If you have any questions or suggestions, feel free to contact us via email or asking a question through our support center.
And check also our education web page where you will find more tutorials!
A look into the future Virtual Research Environment for HADDOCK3
In the context of a project with the Netherlands e-Science Center we are working on building a Virtual Research Environment (VRE) for HADDOCK3 that will allow you to build and edit custom workflows, execute those on a variety of infrastructures (grid, cloud, local, HPC) and provide an interactive analysis platform for analyzing your HADDOCK3 results. This is work in progress but you can already take a glimpse of the first component, the workflow builder, here.
All the HADDOCK3 VRE software development is open and can be followed from our GitHub i-VRESSE repository.
So stay tuned!

